Logarithms and Logistic Growth

Learning Outcomes

  • Evaluate and rewrite logarithms using the properties of logarithms
  • Use the properties of logarithms to solve exponential models for time
  • Identify the carrying capacity in a logistic growth model
  • Use a logistic growth model to predict growth

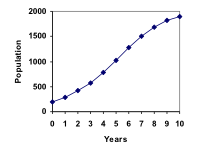
In a confined environment the growth rate of a population may not remain constant. In a lake, for example, there is some maximum sustainable population of fish, also called a carrying capacity. In this section, we will develop a model that contains a carrying capacity term, and use it to predict growth under constraints.  Because resources are typically limited in systems, these types of models are much more common than linear or geometric growth.

The famous Mandelbrot set, a fractal whose growth is constrained.

The famous Mandelbrot set, a fractal whose growth is constrained.

 

Solve Exponentials for Time: Logarithms

Reversing an Exponent

Earlier, we found that since Olympia, WA had a population of 245 thousand in 2008 and had been growing at 3% per year, the population could be modeled by the equation

P­n = (1+0.03)n (245,000), or equivalently, P­n = 245,000(1.03)n.

Using this equation, we were able to predict the population in the future.

A soft-focus landscape photo of a crowd of people. Overlaid on top is a dotted red horizontal line and many vertical blue lines rising above and below the dotted red line, to give the impression of a population growth chart.

Suppose we wanted to know when the population of Olympia would reach 400 thousand. Since we are looking for the year n when the population will be 400 thousand, we would need to solve the equation

400,000 = 245,000(1.03)n

Dividing both sides by 245,000 gives

1.6327 = 1.03n

 

One approach to this problem would be to create a table of values, or to use technology to draw a graph to estimate the solution.

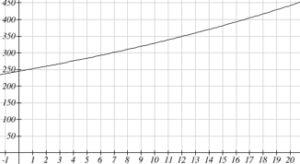
Line graph. Vertical measures increments of 50 from 0 to 450. Horizontal measures increments of 1 from 0 to 20. The line starts at 250/0, and moves in a sloping up trend towards 450/20.

From the graph, we can estimate that the solution will be around 16 to 17 years after 2008 (2024 to 2025). This is pretty good, but we’d really like to have an algebraic tool to answer this question. To do that, we need to introduce a new function that will undo exponentials, similar to how a square root undoes a square. For exponentials, the function we need is called a logarithm. It is the inverse of the exponential, meaning it undoes the exponential. While there is a whole family of logarithms with different bases, we will focus on the common log, which is based on the exponential 10x.

Common Logarithm

The common logarithm, written log(x), undoes the exponential 10x

This means that log(10x) = x, and likewise 10log(x) = x

This also means the statement 10a = b is equivalent to the statement log(b) = a

log(x) is read as “log of x”, and means “the logarithm of the value x”. It is important to note that this is not multiplication – the log doesn’t mean anything by itself, just like √ doesn’t mean anything by itself; it has to be applied to a number.

Example

Evaluate each of the following

  1. log(100)
  2. log(1000)
  3. log(10000)
  4. log(1/100)
  5. log(1)

It is helpful to note that from the first three parts of the previous example that the number we’re taking the log of has to get 10 times bigger for the log to increase in value by 1.

Of course, most numbers cannot be written as a nice simple power of 10. For those numbers, we can evaluate the log using a scientific calculator with a log button.

Example

Evaluate log(300)

With an equation, just like we can add a number to both sides, multiply both sides by a number, or square both sides, we can also take the logarithm of both sides of the equation and end up with an equivalent equation. This will allow us to solve some simple equations.

Examples

  1. Solve 10x = 1000
  2. Solve 10x = 3
  3. Solve 2(10x) = 8

 

This approach allows us to solve exponential equations with powers of 10, but what about problems like 2 = 1.03n from earlier, which have a base of 1.03? For that, we need the exponent property for logs.

Properties of Logs: Exponent Property

[latex]\log\left({{A}^{r}}\right)=r\log\left(A\right)[/latex]

 

To show why this is true, we offer a proof.

Since the logarithm and exponential undo each other, [latex]{{10}^{\log{A}}}=A[/latex].

So [latex]{{A}^{r}}={{\left({{10}^{\log{A}}}\right)}^{r}}[/latex]

Utilizing the exponential rule that states [latex]{{\left({{x}^{a}}\right)}^{b}}={{x}^{ab}}[/latex],

[latex]{{A}^{r}}={{\left({{10}^{\log{A}}}\right)}^{r}}={{10}^{r\log{A}}}[/latex]

 

So then [latex]\log\left({{A}^{r}}\right)=\log\left({{10}^{r\log{A}}}\right)[/latex]

Again utilizing the property that the log undoes the exponential on the right side yields the result

[latex]\log\left({{A}^{r}}\right)=r\log{A}[/latex]

Example

Rewrite log(25) using the exponent property for logs.

 

This property will finally allow us to answer our original question.

Solving exponential equations with logarithms

  1. Isolate the exponential. In other words, get it by itself on one side of the equation. This usually involves dividing by a number multiplying it.
  2. Take the log of both sides of the equation.
  3. Use the exponent property of logs to rewrite the exponential with the variable exponent multiplying the logarithm.
  4. Divide as needed to solve for the variable.

Example

If Olympia is growing according to the equation, P­n = 245(1.03)n, where n is years after 2008, and the population is measured in thousands. Find when the population will be 400 thousand.

A full walkthrough of this problem is available here.

Try It

Alternatively, after applying the exponent property of logs on the right side, we could have evaluated the logarithms to decimal approximations and completed our calculations using those approximations, as you’ll see in the next example. While the final answer may come out slightly differently, as long as we keep enough significant values during calculation, our answer will be close enough for most purposes.

Example

Polluted water is passed through a series of filters. Each filter removes 90% of the remaining impurities from the water. If you have 10 million particles of pollutant per gallon originally, how many filters would the water need to be passed through to reduce the pollutant to 500 particles per gallon?

More details about solving this scenario are available in this video.

 

Try It

India had a population in 2008 of about 1.14 billion people. The population is growing by about 1.34% each year. If this trend continues, when will India’s population reach 1.2 billion?

 

TIP

When you are solving growth problems, use the language in the question to determine whether you are solving for time, future value, present value or growth rate. Questions that uses words like “when”, “what year”, or “how long” are asking you to solve for time and you will need to use logarithms to solve them because the time variable in growth problems is in the exponent.

Logistic Growth

Limits on Exponential Growth

In our basic exponential growth scenario, we had a recursive equation of the form

P­n = P­n-1 + r P­n-1

In a confined environment, however, the growth rate may not remain constant. In a lake, for example, there is some maximum sustainable population of fish, also called a carrying capacity.

Carrying Capacity

The carrying capacity, or maximum sustainable population, is the largest population that an environment can support.

Dense koi fish population in water

For our fish, the carrying capacity is the largest population that the resources in the lake can sustain. If the population in the lake is far below the carrying capacity, then we would expect the population to grow essentially exponentially. However, as the population approaches the carrying capacity, there will be a scarcity of food and space available, and the growth rate will decrease. If the population exceeds the carrying capacity, there won’t be enough resources to sustain all the fish and there will be a negative growth rate, causing the population to decrease back to the carrying capacity.

If the carrying capacity was 5000, the growth rate might vary something like that in the graph shown.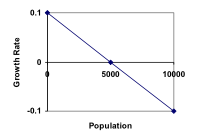Graph. Vertical measures Growth Rate, in increments of .1, from -0.1 to 0.1. Horizontal measures Population, in increments of 5000, from 0 to 10000. There's a diagonal line sloping down from 0.1 at 0 to -0.1 at 10000.

Note that this is a linear equation with intercept at 0.1 and slope [latex]-\frac{0.1}{5000}[/latex], so we could write an equation for this adjusted growth rate as:

radjusted = [latex]0.1-\frac{0.1}{5000}P=0.1\left(1-\frac{P}{5000}\right)[/latex]

Substituting this in to our original exponential growth model for r gives

[latex]{{P}_{n}}={{P}_{n-1}}+0.1\left(1-\frac{{{P}_{n-1}}}{5000}\right){{P}_{n-1}}[/latex]

View the following for a detailed explanation of the concept.

Logistic Growth

If a population is growing in a constrained environment with carrying capacity K, and absent constraint would grow exponentially with growth rate r, then the population behavior can be described by the logistic growth model:

[latex]{{P}_{n}}={{P}_{n-1}}+r\left(1-\frac{{{P}_{n-1}}}{K}\right){{P}_{n-1}}[/latex]

Unlike linear and exponential growth, logistic growth behaves differently if the populations grow steadily throughout the year or if they have one breeding time per year. The recursive formula provided above models generational growth, where there is one breeding time per year (or, at least a finite number); there is no explicit formula for this type of logistic growth.

Examples

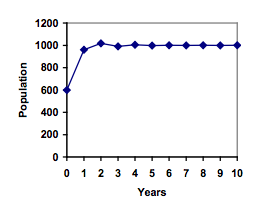
A forest is currently home to a population of 200 rabbits. The forest is estimated to be able to sustain a population of 2000 rabbits. Absent any restrictions, the rabbits would grow by 50% per year. Predict the future population using the logistic growth model.

View more about this example below.

On an island that can support a population of 1000 lizards, there is currently a population of 600. These lizards have a lot of offspring and not a lot of natural predators, so have very high growth rate, around 150%. Calculating out the next couple generations:

[latex]{{P}_{1}}={{P}_{0}}+1.50\left(1-\frac{{{P}_{0}}}{1000}\right){{P}_{0}}=600+1.50\left(1-\frac{600}{1000}\right)600=960[/latex]

[latex]{{P}_{2}}={{P}_{1}}+1.50\left(1-\frac{{{P}_{1}}}{1000}\right){{P}_{1}}=960+1.50\left(1-\frac{960}{1000}\right)960=1018[/latex]

Interestingly, even though the factor that limits the growth rate slowed the growth a lot, the population still overshot the carrying capacity. We would expect the population to decline the next year.

[latex]{{P}_{3}}={{P}_{2}}+1.50\left(1-\frac{{{P}_{3}}}{1000}\right){{P}_{3}}=1018+1.50\left(1-\frac{1018}{1000}\right)1018=991[/latex]

Calculating out a few more years and plotting the results, we see the population wavers above and below the carrying capacity, but eventually settles down, leaving a steady population near the carrying capacity.

Graph. Vertical measures Population, in increments of 200 from 0 to 1200. Horizontal measures Years, in increments of 1 from 0 to 10. Year 0 shows population of 600, jumping to ~1000 in year 1, a little over 1000 in year 2, and staying close to 1000 in every subsequent year.

 

Try It

A field currently contains 20 mint plants. Absent constraints, the number of plants would increase by 70% each year, but the field can only support a maximum population of 300 plants. Use the logistic model to predict the population in the next three years.

Example

On a neighboring island to the one from the previous example, there is another population of lizards, but the growth rate is even higher – about 205%.

Calculating out several generations and plotting the results, we get a surprise: the population seems to be oscillating between two values, a pattern called a 2-cycle.Graph. Vertical measures Population, in increments of 200 from 0 to 1200. Horizontal measures Years, in increments of 1 from 0 to 10. Year 0 shows population of 600, jumping to ~1100 in year 1, down to ~900 in year 2, and vacillating from 1100 to 800 in alternating years through the rest of the graph.

While it would be tempting to treat this only as a strange side effect of mathematics, this has actually been observed in nature. Researchers from the University of California observed a stable 2-cycle in a lizard population in California.[1]

Taking this even further, we get more and more extreme behaviors as the growth rate increases higher. It is possible to get stable 4-cycles, 8-cycles, and higher. Quickly, though, the behavior approaches chaos (remember the movie Jurassic Park?).

Two graphs. Left graph, labeled “r=2.46 A 4-cycle.” Vertical measures Population, in increments of 200 from 0 to 1400. Horizontal measures Years, in increments of 1 from 0 to 10. The plotted line moves in sharp up and down cycles, from ~700 in year 0, 1200 in year 1, 600 in year 2, 1200 in year 3, ~600 in year 4, and so forth. Right graph, labeled “r=2.9 Chaos!” Vertical measures Population, in increments of 200 from 0 to 1400. Horizontal measures Years, in increments of 5 from 0 to 30. The plotted line moves in sharp up and down cycles of varying lengths, forming an erratic back and forth between highs and lows.

All of the lizard island examples are discussed in this video.

Try It

  1. http://users.rcn.com/jkimball.ma.ultranet/BiologyPages/P/Populations2.html ↵