More Function Types

Learning Outcomes

  • Identify a rational function
  • Describe the graphs of power and root functions
  • Explain the difference between algebraic and transcendental functions
  • Graph a piecewise-defined function

Algebraic Functions

By allowing for quotients and fractional powers in polynomial functions, we create a larger class of functions. An algebraic function is one that involves addition, subtraction, multiplication, division, rational powers, and roots. Two types of algebraic functions are rational functions and root functions.

Just as rational numbers are quotients of integers, rational functions are quotients of polynomials. In particular, a rational function is any function of the form [latex]f(x)=p(x)/q(x)[/latex], where [latex]p(x)[/latex] and [latex]q(x)[/latex] are polynomials. For example,

[latex]f(x)=\dfrac{3x-1}{5x+2}[/latex]  and   [latex]g(x)=\dfrac{4}{x^2+1}[/latex]

 

are rational functions. A root function is a power function of the form [latex]f(x)=x^{1/n}[/latex], where [latex]n[/latex] is a positive integer greater than one. For example, [latex]f(x)=x^{1/2}=\sqrt{x}[/latex] is the square-root function and [latex]g(x)=x^{1/3}=\sqrt[3]{x}[/latex] is the cube-root function. By allowing for compositions of root functions and rational functions, we can create other algebraic functions. For example, [latex]f(x)=\sqrt{4-x^2}[/latex] is an algebraic function.

Example: Finding Domain and Range for Algebraic Functions

For each of the following functions, find the domain and range.

  1. [latex]f(x)=\dfrac{3x-1}{5x+2}[/latex]
  2. [latex]f(x)=\sqrt{4-x^2}[/latex]

 

Try It

Find the domain and range for the function [latex]f(x)=\dfrac{(5x+2)}{(2x-1)}[/latex].

 

 

The root functions [latex]f(x)=x^{1/n}[/latex] have defining characteristics depending on whether [latex]n[/latex] is odd or even. For all even integers [latex]n \ge 2[/latex], the domain of [latex]f(x)=x^{1/n}[/latex] is the interval [latex][0,\infty)[/latex]. For all odd integers [latex]n \ge 1[/latex], the domain of [latex]f(x)=x^{1/n}[/latex] is the set of all real numbers. Since [latex]x^{1/n}=(−x)^{1/n}[/latex] for odd integers [latex]n, \, f(x)=x^{1/n}[/latex] is an odd function if [latex]n[/latex] is odd. See the graphs of root functions for different values of [latex]n[/latex] in Figure 11.

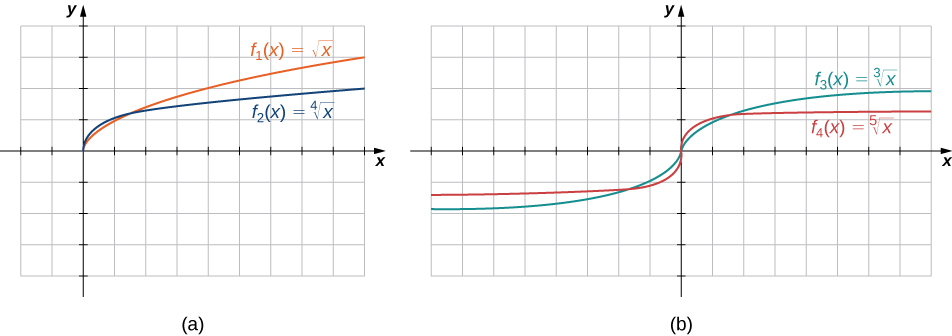
An image of two graphs. The first graph is labeled “a” and has an x axis that runs from -2 to 9 and a y axis that runs from -4 to 4. The first graph is of two functions. The first function is “f(x) = square root of x”, which is a curved function that begins at the origin and increases. The second function is “f(x) = x to the 4th root”, which is a curved function that begins at the origin and increases, but increases at a slower rate than the first function. The second graph is labeled “b” and has an x axis that runs from -8 to 8 and a y axis that runs from -4 to 4. The second graph is of two functions. The first function is “f(x) = cube root of x”, which is a curved function that increases until the origin, becomes vertical at the origin, and then increases again after the origin. The second function is “f(x) = x to the 5th root”, which is a curved function that increases until the origin, becomes vertical at the origin, and then increases again after the origin, but increases at a slower rate than the first function.

Figure 11. (a) If [latex]n[/latex] is even, the domain of [latex]f(x)=\sqrt[n]{x}[/latex] is [latex][0,\infty)[/latex]. (b) If [latex]n[/latex] is odd, the domain of [latex]f(x)=\sqrt[n]{x}[/latex] is [latex](-\infty,\infty )[/latex] and the function [latex]f(x)=\sqrt[n]{x}[/latex] is an odd function.

Example: Finding Domains for Algebraic Functions

For each of the following functions, determine the domain of the function.

  1. [latex]f(x)=\dfrac{3}{x^2-1}[/latex]
  2. [latex]f(x)=\dfrac{2x+5}{3x^2+4}[/latex]
  3. [latex]f(x)=\sqrt{4-3x}[/latex]
  4. [latex]f(x)=\sqrt[3]{2x-1}[/latex]

 

Try It

Find the domain for each of the following functions: [latex]f(x)=\dfrac{(5-2x)}{(x^2+2)}[/latex] and [latex]g(x)=\sqrt{5x-1}[/latex].

 

 

Transcendental Functions

Thus far, we have discussed algebraic functions. Some functions, however, cannot be described by basic algebraic operations. These functions are known as transcendental functions because they are said to “transcend,” or go beyond, algebra. The most common transcendental functions are trigonometric, exponential, and logarithmic functions. A trigonometric function relates the ratios of two sides of a right triangle. They are [latex]\sin x,\, \cos x, \, \tan x, \, \cot x,\, \sec x[/latex], and [latex]\csc x[/latex]. (We discuss trigonometric functions later in the module.) An exponential function is a function of the form [latex]f(x)=b^x[/latex], where the base [latex]b>0, \, b \ne 1[/latex]. A logarithmic function is a function of the form [latex]f(x)=\log_b(x)[/latex] for some constant [latex]b>0, \, b \ne 1[/latex], where [latex]\log_b(x)=y[/latex] if and only if [latex]b^y=x[/latex]. (We also discuss exponential and logarithmic functions later in the module.)

Example: Classifying Algebraic and Transcendental Functions

Classify each of the following functions, a. through c., as algebraic or transcendental.

  1. [latex]f(x)= \dfrac{\sqrt{x^3+1}}{4x+2}[/latex]
  2. [latex]f(x)=2^{x^2}[/latex]
  3. [latex]f(x)=\sin (2x)[/latex]

 

Watch the following video to see the worked solution to Example: Classifying Algebraic and Transcendental Functions

Try It

Is [latex]f(x)=\dfrac{x}{2}[/latex] an algebraic or a transcendental function?

 

Piecewise-Defined Functions

Sometimes a function is defined by different formulas on different parts of its domain. A function with this property is known as a piecewise-defined function. The absolute value function is an example of a piecewise-defined function because the formula changes with the sign of [latex]x[/latex]:

[latex]f(x)=\begin{cases} x, & x \ge 0 \\ -x, & x < 0 \end{cases}[/latex]

Other piecewise-defined functions may be represented by completely different formulas, depending on the part of the domain in which a point falls. To graph a piecewise-defined function, we graph each part of the function in its respective domain, on the same coordinate system. If the formula for a function is different for [latex]xa[/latex], we need to pay special attention to what happens at [latex]x=a[/latex] when we graph the function. Sometimes the graph needs to include an open or closed circle to indicate the value of the function at [latex]x=a[/latex]. We examine this in the next example. If you need a refresher, check out the Recall box first.

Recall: Given a piecewise function, sketch a graph.

  1. Indicate on the [latex]x[/latex]-axis the boundaries defined by the intervals on each piece of the domain.
  2. For each piece of the domain, graph on that interval using the corresponding equation pertaining to that piece. Do not graph two functions over one interval because it would violate the criteria of a function.

Example: Graphing a Piecewise-Defined Function

Sketch a graph of the following piecewise-defined function:

[latex]f(x)=\begin{cases} x+3, & x < 1 \\ (x-2)^2 & x \ge 1 \end{cases}[/latex]  

Try It

Sketch a graph of the function

[latex]f(x)=\begin{cases} 2-x, & x \le 2 \\ x+2, & x>2 \end{cases}[/latex]

 

Example: Parking Fees Described by a Piecewise-Defined Function

In a big city, drivers are charged variable rates for parking in a parking garage. They are charged $10 for the first hour or any part of the first hour and an additional $2 for each hour or part thereof up to a maximum of $30 for the day. The parking garage is open from 6 a.m. to 12 midnight.

  1. Write a piecewise-defined function that describes the cost [latex]C[/latex] to park in the parking garage as a function of hours parked [latex]x[/latex].
  2. Sketch a graph of this function [latex]C(x)[/latex].

 

Watch the following video to see the worked solution to Example: Parking Fees Described by a Piecewise-Defined Function

Try It

The cost of mailing a letter is a function of the weight of the letter. Suppose the cost of mailing a letter is [latex]49\text{¢}[/latex] for the first ounce and [latex]21\text{¢}[/latex] for each additional ounce. Write a piecewise-defined function describing the cost [latex]C[/latex] as a function of the weight [latex]x[/latex] for [latex]0 < x \le 3[/latex], where [latex]C[/latex] is measured in cents and [latex]x[/latex] is measured in ounces.

 

 

Try It