Learning Outcomes
- Recognize a parabola, ellipse, or hyperbola from its eccentricity value
- Write the polar equation of a conic section with eccentricity [latex]e[/latex]
- Identify when a general equation of degree two is a parabola, ellipse, or hyperbola
Eccentricity and Directrix
An alternative way to describe a conic section involves the directrices, the foci, and a new property called eccentricity. We will see that the value of the eccentricity of a conic section can uniquely define that conic.
Definition
The eccentricity e of a conic section is defined to be the distance from any point on the conic section to its focus, divided by the perpendicular distance from that point to the nearest directrix. This value is constant for any conic section, and can define the conic section as well:
- If [latex]e=1[/latex], the conic is a parabola.
- If [latex]e<1[/latex], it is an ellipse.
- If [latex]e>1[/latex], it is a hyperbola.
The eccentricity of a circle is zero. The directrix of a conic section is the line that, together with the point known as the focus, serves to define a conic section. Hyperbolas and noncircular ellipses have two foci and two associated directrices. Parabolas have one focus and one directrix.
The three conic sections with their directrices appear in the following figure.
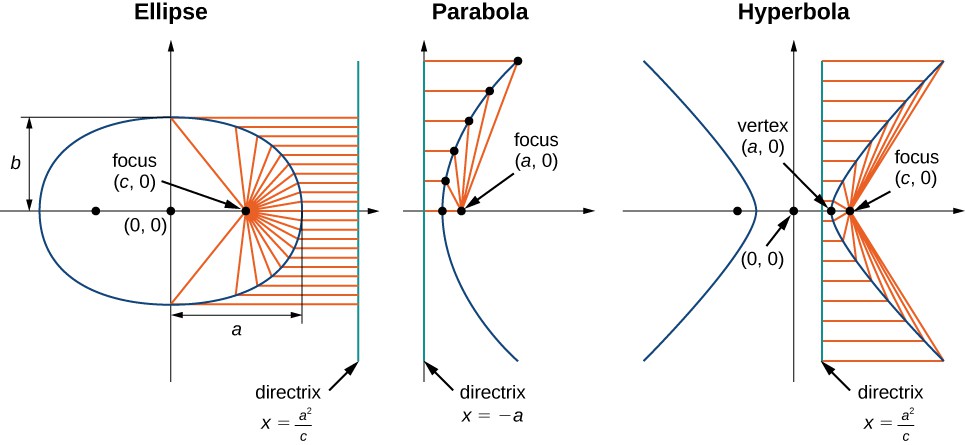
Figure 16. The three conic sections with their foci and directrices.
Recall from the definition of a parabola that the distance from any point on the parabola to the focus is equal to the distance from that same point to the directrix. Therefore, by definition, the eccentricity of a parabola must be 1. The equations of the directrices of a horizontal ellipse are [latex]x=\pm \frac{{a}^{2}}{c}[/latex]. The right vertex of the ellipse is located at [latex]\left(a,0\right)[/latex] and the right focus is [latex]\left(c,0\right)[/latex]. Therefore the distance from the vertex to the focus is [latex]a-c[/latex] and the distance from the vertex to the right directrix is [latex]\frac{{a}^{2}}{c}-c[/latex]. This gives the eccentricity as
Since [latex]c<a[/latex], this step proves that the eccentricity of an ellipse is less than 1. The directrices of a horizontal hyperbola are also located at [latex]x=\pm \frac{{a}^{2}}{c}[/latex], and a similar calculation shows that the eccentricity of a hyperbola is also [latex]e=\frac{c}{a}[/latex]. However in this case we have [latex]c>a[/latex], so the eccentricity of a hyperbola is greater than 1.
Example: Determining Eccentricity of a Conic Section
Determine the eccentricity of the ellipse described by the equation
Watch the following video to see the worked solution to Example: Determining Eccentricity of a Conic Section.
For closed captioning, open the video on its original page by clicking the Youtube logo in the lower right-hand corner of the video display. In YouTube, the video will begin at the same starting point as this clip, but will continue playing until the very end.
You can view the transcript for this segmented clip of “7.5 Conic Sections” here (opens in new window).
try it
Determine the eccentricity of the hyperbola described by the equation
Try It
Polar Equations of Conic Sections
Sometimes it is useful to write or identify the equation of a conic section in polar form. To do this, we need the concept of the focal parameter. The focal parameter of a conic section p is defined as the distance from a focus to the nearest directrix. The following table gives the focal parameters for the different types of conics, where a is the length of the semi-major axis (i.e., half the length of the major axis), c is the distance from the origin to the focus, and e is the eccentricity. In the case of a parabola, a represents the distance from the vertex to the focus.
| Conic | e | p |
|---|---|---|
| Ellipse | [latex]0<e<1[/latex] | [latex]\frac{{a}^{2}-{c}^{2}}{c}=\frac{a\left(1-{e}^{2}\right)}{c}[/latex] |
| Parabola | [latex]e=1[/latex] | [latex]2a[/latex] |
| Hyperbola | [latex]e>1[/latex] | [latex]\frac{{c}^{2}-{a}^{2}}{c}=\frac{a\left({e}^{2}-1\right)}{e}[/latex] |
Using the definitions of the focal parameter and eccentricity of the conic section, we can derive an equation for any conic section in polar coordinates. In particular, we assume that one of the foci of a given conic section lies at the pole. Then using the definition of the various conic sections in terms of distances, it is possible to prove the following theorem.
theorem: Polar Equation of Conic Sections
The polar equation of a conic section with focal parameter p is given by
In the equation on the left, the major axis of the conic section is horizontal, and in the equation on the right, the major axis is vertical. To work with a conic section written in polar form, first make the constant term in the denominator equal to 1. This can be done by dividing both the numerator and the denominator of the fraction by the constant that appears in front of the plus or minus in the denominator. Then the coefficient of the sine or cosine in the denominator is the eccentricity. This value identifies the conic. If cosine appears in the denominator, then the conic is horizontal. If sine appears, then the conic is vertical. If both appear then the axes are rotated. The center of the conic is not necessarily at the origin. The center is at the origin only if the conic is a circle (i.e., [latex]e=0[/latex]).
Example: Graphing a Conic Section in Polar Coordinates
Identify and create a graph of the conic section described by the equation
Watch the following video to see the worked solution to Example: Graphing a Conic Section in Polar Coordinates.
For closed captioning, open the video on its original page by clicking the Youtube logo in the lower right-hand corner of the video display. In YouTube, the video will begin at the same starting point as this clip, but will continue playing until the very end.
You can view the transcript for this segmented clip of “7.5 Conic Sections” here (opens in new window).
try it
Identify and create a graph of the conic section described by the equation
Try It
General Equations of Degree Two
A general equation of degree two can be written in the form
The graph of an equation of this form is a conic section. If [latex]B\ne 0[/latex] then the coordinate axes are rotated. To identify the conic section, we use the discriminant of the conic section [latex]4AC-{B}^{2}[/latex]. One of the following cases must be true:
- [latex]4AC-{B}^{2}>0[/latex]. If so, the graph is an ellipse.
- [latex]4AC-{B}^{2}=0[/latex]. If so, the graph is a parabola.
- [latex]4AC-{B}^{2}<0[/latex]. If so, the graph is a hyperbola.
The simplest example of a second-degree equation involving a cross term is [latex]xy=1[/latex]. This equation can be solved for y to obtain [latex]y=\frac{1}{x}[/latex]. The graph of this function is called a rectangular hyperbola as shown.
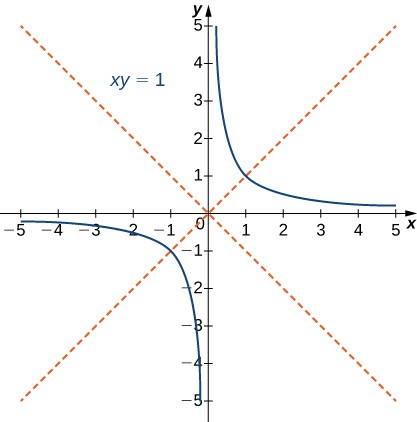
Figure 19. Graph of the equation [latex]xy=1[/latex]; The red lines indicate the rotated axes.
The asymptotes of this hyperbola are the x and y coordinate axes. To determine the angle [latex]\theta [/latex] of rotation of the conic section, we use the formula [latex]\cot{2\theta}=\frac{A-C}{B}[/latex]. In this case [latex]A=C=0[/latex] and [latex]B=1[/latex], so [latex]\cot{2\theta}=\frac{\left(0 - 0\right)}{1}=0[/latex] and [latex]\theta =45^\circ[/latex]. The method for graphing a conic section with rotated axes involves determining the coefficients of the conic in the rotated coordinate system. The new coefficients are labeled [latex]{A}^{\prime },{B}^{\prime },{C}^{\prime },{D}^{\prime },{E}^{\prime },\text{ and }{F}^{\prime }[/latex], and are given by the formulas
The procedure for graphing a rotated conic is the following:
- Identify the conic section using the discriminant [latex]4AC-{B}^{2}[/latex].
- Determine [latex]\theta [/latex] using the formula [latex]\cot2\theta =\frac{A-C}{B}[/latex].
- Calculate [latex]{A}^{\prime },{B}^{\prime },{C}^{\prime },{D}^{\prime },{E}^{\prime },\text{and}{F}^{\prime }[/latex].
- Rewrite the original equation using [latex]{A}^{\prime },{B}^{\prime },{C}^{\prime },{D}^{\prime },{E}^{\prime },\text{and}{F}^{\prime }[/latex].
- Draw a graph using the rotated equation.
Example: Identifying a Rotated Conic
Identify the conic and calculate the angle of rotation of axes for the curve described by the equation
Watch the following video to see the worked solution to Example: Identifying a Rotated Conic.
For closed captioning, open the video on its original page by clicking the Youtube logo in the lower right-hand corner of the video display. In YouTube, the video will begin at the same starting point as this clip, but will continue playing until the very end.
You can view the transcript for this segmented clip of “7.5 Conic Sections” here (opens in new window).
try it
Identify the conic and calculate the angle of rotation of axes for the curve described by the equation



