Parabolas

A parabola is generated when a plane intersects a cone parallel to the generating line. In this case, the plane intersects only one of the nappes. A parabola can also be defined in terms of distances.

A graph of a typical parabola appears in Figure 3. Using this diagram in conjunction with the distance formula, we can derive an equation for a parabola. Recall the distance formula: Given point P with coordinates [latex]\left({x}_{1},{y}_{1}\right)[/latex] and point Q with coordinates [latex]\left({x}_{2},{\text{y}}_{2}\right)[/latex], the distance between them is given by the formula

Then from the definition of a parabola and Figure 3, we get

Squaring both sides and simplifying yields

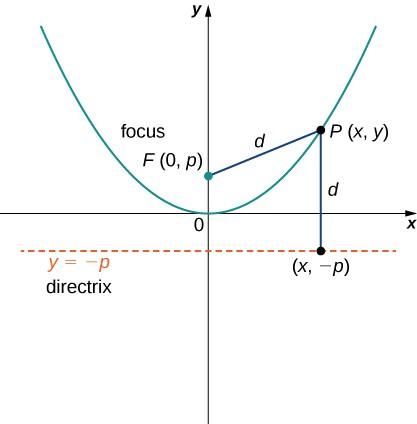
Figure 3. A typical parabola in which the distance from the focus to the vertex is represented by the variable [latex]p[/latex].

Now suppose we want to relocate the vertex. We use the variables [latex]\left(h,k\right)[/latex] to denote the coordinates of the vertex. Then if the focus is directly above the vertex, it has coordinates [latex]\left(h,k+p\right)[/latex] and the directrix has the equation [latex]y=k-p[/latex]. Going through the same derivation yields the formula [latex]{\left(x-h\right)}^{2}=4p\left(y-k\right)[/latex]. Solving this equation for y leads to the following theorem.

We can also study the cases when the parabola opens down or to the left or the right. The equation for each of these cases can also be written in standard form as shown in the following graphs.

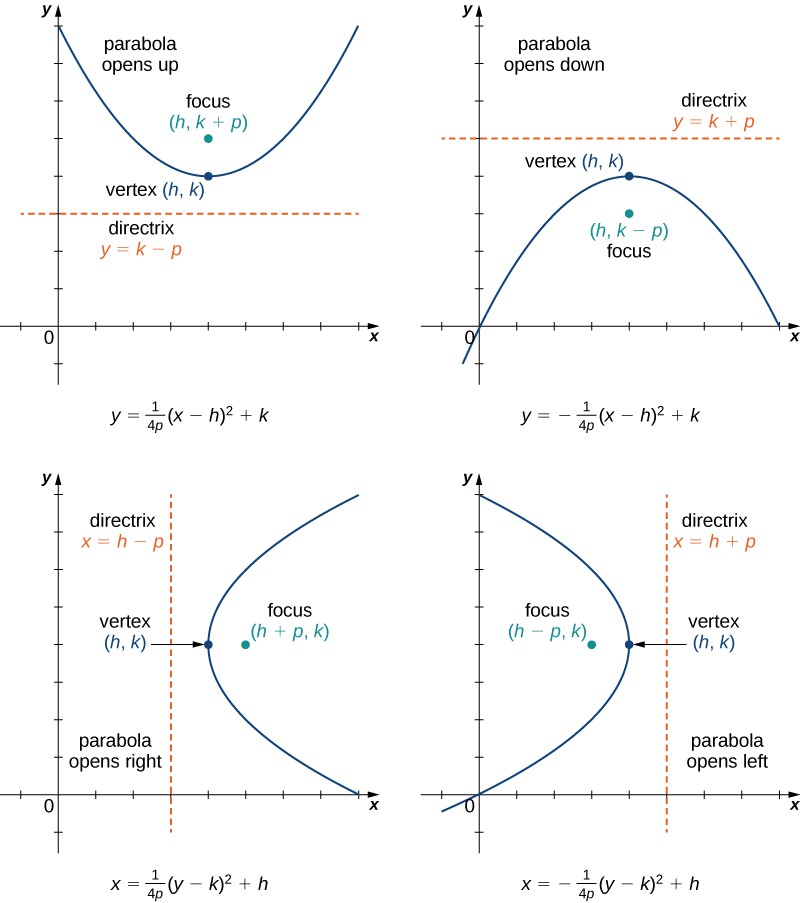
Figure 4. Four parabolas, opening in various directions, along with their equations in standard form.

In addition, the equation of a parabola can be written in the general form, though in this form the values of h, k, and p are not immediately recognizable. The general form of a parabola is written as

The first equation represents a parabola that opens either up or down. The second equation represents a parabola that opens either to the left or to the right. To put the equation into standard form, use the method of completing the square.

Example: Converting the Equation of a Parabola from General into Standard Form

Put the equation [latex]{x}^{2}-4x - 8y+12=0[/latex] into standard form and graph the resulting parabola.

Show Solution

Since y is not squared in this equation, we know that the parabola opens either upward or downward. Therefore we need to solve this equation for y, which will put the equation into standard form. To do that, first add [latex]8y[/latex] to both sides of the equation:

[latex]8y={x}^{2}-4x+12[/latex].

 

The next step is to complete the square on the right-hand side. Start by grouping the first two terms on the right-hand side using parentheses:

[latex]8y=\left({x}^{2}-4x\right)+12[/latex].

 

Next determine the constant that, when added inside the parentheses, makes the quantity inside the parentheses a perfect square trinomial. To do this, take half the coefficient of x and square it. This gives [latex]{\left(\frac{-4}{2}\right)}^{2}=4[/latex]. Add 4 inside the parentheses and subtract 4 outside the parentheses, so the value of the equation is not changed:

[latex]8y=\left({x}^{2}-4x+4\right)+12 - 4[/latex].

 

Now combine like terms and factor the quantity inside the parentheses:

[latex]8y={\left(x - 2\right)}^{2}+8[/latex].

Finally, divide by 8:

[latex]y=\frac{1}{8}{\left(x - 2\right)}^{2}+1[/latex].

 

This equation is now in standard form. Comparing this to equations for parabolas gives [latex]h=2[/latex], [latex]k=1[/latex], and [latex]p=2[/latex]. The parabola opens up, with vertex at [latex]\left(2,1\right)[/latex], focus at [latex]\left(2,3\right)[/latex], and directrix [latex]y=-1[/latex]. The graph of this parabola appears as follows.

Figure 5. The parabola in [link].

Watch the following video to see the worked solution to Example: Converting the Equation of a Parabola from General into Standard Form.

For closed captioning, open the video on its original page by clicking the Youtube logo in the lower right-hand corner of the video display. In YouTube, the video will begin at the same starting point as this clip, but will continue playing until the very end.

You can view the transcript for this segmented clip of “7.5 Conic Sections” here (opens in new window).

try it

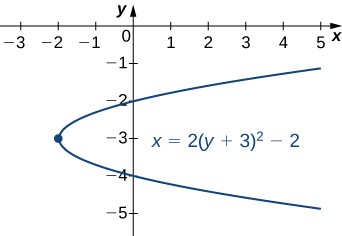
Put the equation [latex]2{y}^{2}-x+12y+16=0[/latex] into standard form and graph the resulting parabola.

Hint

Solve for x. Check which direction the parabola opens.

Show Solution

[latex]x=2{\left(y+3\right)}^{2}-2[/latex]

Figure 6.

The axis of symmetry of a vertical (opening up or down) parabola is a vertical line passing through the vertex. The parabola has an interesting reflective property. Suppose we have a satellite dish with a parabolic cross section. If a beam of electromagnetic waves, such as light or radio waves, comes into the dish in a straight line from a satellite (parallel to the axis of symmetry), then the waves reflect off the dish and collect at the focus of the parabola as shown.

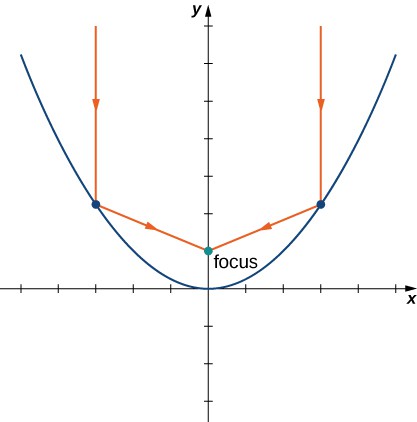
Figure 7.

Consider a parabolic dish designed to collect signals from a satellite in space. The dish is aimed directly at the satellite, and a receiver is located at the focus of the parabola. Radio waves coming in from the satellite are reflected off the surface of the parabola to the receiver, which collects and decodes the digital signals. This allows a small receiver to gather signals from a wide angle of sky. Flashlights and headlights in a car work on the same principle, but in reverse: the source of the light (that is, the light bulb) is located at the focus and the reflecting surface on the parabolic mirror focuses the beam straight ahead. This allows a small light bulb to illuminate a wide angle of space in front of the flashlight or car.

Ellipses

An ellipse can also be defined in terms of distances. In the case of an ellipse, there are two foci (plural of focus), and two directrices (plural of directrix). We look at the directrices in more detail later in this section.

Definition

---

An ellipse is the set of all points for which the sum of their distances from two fixed points (the foci) is constant.

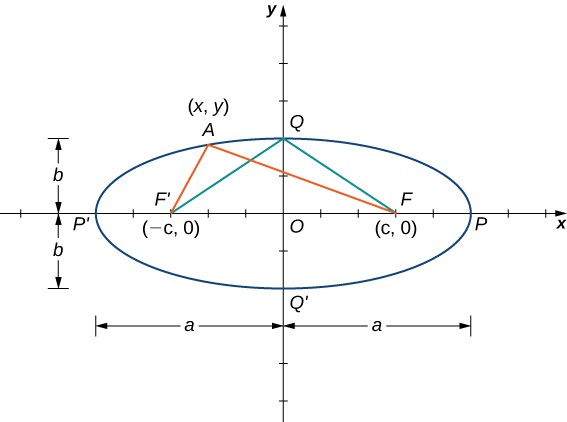
Figure 8. A typical ellipse in which the sum of the distances from any point on the ellipse to the foci is constant.

A graph of a typical ellipse is shown in Figure 8. In this figure the foci are labeled as [latex]F[/latex] and [latex]{F}^{\prime }[/latex]. Both are the same fixed distance from the origin, and this distance is represented by the variable c. Therefore the coordinates of [latex]F[/latex] are [latex]\left(c,0\right)[/latex] and the coordinates of [latex]{F}^{\prime }[/latex] are [latex]\left(-c,0\right)[/latex]. The points [latex]P[/latex] and [latex]{P}^{\prime }[/latex] are located at the ends of the major axis of the ellipse, and have coordinates [latex]\left(a,0\right)[/latex] and [latex]\left(-a,0\right)[/latex], respectively. The major axis is always the longest distance across the ellipse, and can be horizontal or vertical. Thus, the length of the major axis in this ellipse is 2a. Furthermore, [latex]P[/latex] and [latex]{P}^{\prime }[/latex] are called the vertices of the ellipse. The points [latex]Q[/latex] and [latex]{Q}^{\prime }[/latex] are located at the ends of the minor axis of the ellipse, and have coordinates [latex]\left(0,b\right)[/latex] and [latex]\left(0,-b\right)[/latex], respectively. The minor axis is the shortest distance across the ellipse. The minor axis is perpendicular to the major axis.

According to the definition of the ellipse, we can choose any point on the ellipse and the sum of the distances from this point to the two foci is constant. Suppose we choose the point P. Since the coordinates of point P are [latex]\left(a,0\right)[/latex], the sum of the distances is

[latex]d\left(P,F\right)+d\left(P,{F}^{\prime }\right)=\left(a-c\right)+\left(a+c\right)=2a[/latex].

 

Therefore the sum of the distances from an arbitrary point A with coordinates [latex]\left(x,y\right)[/latex] is also equal to [latex]2a[/latex]. Using the distance formula, we get

[latex]\begin{array}{ccc}\hfill d\left(A,F\right)+d\left(A,{F}^{\prime }\right)& =\hfill & 2a\hfill \\ \hfill \sqrt{{\left(x-c\right)}^{2}+{y}^{2}}+\sqrt{{\left(x+c\right)}^{2}+{y}^{2}}& =\hfill & 2a.\hfill \end{array}[/latex]

 

Subtract the second radical from both sides and square both sides:

[latex]\begin{array}{ccc}\hfill \sqrt{{\left(x-c\right)}^{2}+{y}^{2}}& =\hfill & 2a-\sqrt{{\left(x+c\right)}^{2}+{y}^{2}}\hfill \\ \hfill {\left(x-c\right)}^{2}+{y}^{2}& =\hfill & 4{a}^{2}-4a\sqrt{{\left(x+c\right)}^{2}+{y}^{2}}+{\left(x+c\right)}^{2}+{y}^{2}\hfill \\ \hfill {x}^{2}-2cx+{c}^{2}+{y}^{2}& =\hfill & 4{a}^{2}-4a\sqrt{{\left(x+c\right)}^{2}+{y}^{2}}+{x}^{2}+2cx+{c}^{2}+{y}^{2}\hfill \\ \hfill -2cx& =\hfill & 4{a}^{2}-4a\sqrt{{\left(x+c\right)}^{2}+{y}^{2}}+2cx.\hfill \end{array}[/latex]

 

Now isolate the radical on the right-hand side and square again:

[latex]\begin{array}{ccc}\hfill -2cx& =\hfill & 4{a}^{2}-4a\sqrt{{\left(x+c\right)}^{2}+{y}^{2}}+2cx\hfill \\ \hfill 4a\sqrt{{\left(x+c\right)}^{2}+{y}^{2}}& =\hfill & 4{a}^{2}+4cx\hfill \\ \hfill \sqrt{{\left(x+c\right)}^{2}+{y}^{2}}& =\hfill & a+\frac{cx}{a}\hfill \\ \hfill {\left(x+c\right)}^{2}+{y}^{2}& =\hfill & {a}^{2}+2cx+\frac{{c}^{2}{x}^{2}}{{a}^{2}}\hfill \\ \hfill {x}^{2}+2cx+{c}^{2}+{y}^{2}& =\hfill & {a}^{2}+2cx+\frac{{c}^{2}{x}^{2}}{{a}^{2}}\hfill \\ \hfill {x}^{2}+{c}^{2}+{y}^{2}& =\hfill & {a}^{2}+\frac{{c}^{2}{x}^{2}}{{a}^{2}}.\hfill \end{array}[/latex]

 

Isolate the variables on the left-hand side of the equation and the constants on the right-hand side:

[latex]\begin{array}{}\\ \hfill {x}^{2}-\frac{{c}^{2}{x}^{2}}{{a}^{2}}+{y}^{2}& =\hfill & {a}^{2}-{c}^{2}\hfill \\ \hfill \frac{\left({a}^{2}-{c}^{2}\right){x}^{2}}{{a}^{2}}+{y}^{2}& =\hfill & {a}^{2}-{c}^{2}.\hfill \end{array}[/latex]

 

Divide both sides by [latex]{a}^{2}-{c}^{2}[/latex]. This gives the equation

[latex]\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{a}^{2}-{c}^{2}}=1[/latex].

 

If we refer back to Figure 8, then the length of each of the two green line segments is equal to a. This is true because the sum of the distances from the point Q to the foci [latex]F\text{and}{F}^{\prime }[/latex] is equal to 2a, and the lengths of these two line segments are equal. This line segment forms a right triangle with hypotenuse length a and leg lengths b and c. From the Pythagorean theorem, [latex]{a}^{2}+{b}^{2}={c}^{2}[/latex] and [latex]{b}^{2}={a}^{2}-{c}^{2}[/latex]. Therefore the equation of the ellipse becomes

[latex]\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1[/latex].

 

Finally, if the center of the ellipse is moved from the origin to a point [latex]\left(h,k\right)[/latex], we have the following standard form of an ellipse.

theorem: Equation of an Ellipse in Standard Form

---

Consider the ellipse with center [latex]\left(h,k\right)[/latex], a horizontal major axis with length [latex]2a[/latex], and a vertical minor axis with length [latex]2b[/latex]. Then the equation of this ellipse in standard form is

[latex]\frac{{\left(x-h\right)}^{2}}{{a}^{2}}+\frac{{\left(y-k\right)}^{2}}{{b}^{2}}=1[/latex]

 

and the foci are located at [latex]\left(h\pm c,k\right)[/latex], where [latex]{c}^{2}={a}^{2}-{b}^{2}[/latex]. The equations of the directrices are [latex]x=h\pm \frac{{a}^{2}}{c}[/latex].

If the major axis is vertical, then the equation of the ellipse becomes

[latex]\frac{{\left(x-h\right)}^{2}}{{b}^{2}}+\frac{{\left(y-k\right)}^{2}}{{a}^{2}}=1[/latex]

 

and the foci are located at [latex]\left(h,k\pm c\right)[/latex], where [latex]{c}^{2}={a}^{2}-{b}^{2}[/latex]. The equations of the directrices in this case are [latex]y=k\pm \frac{{a}^{2}}{c}[/latex].

If the major axis is horizontal, then the ellipse is called horizontal, and if the major axis is vertical, then the ellipse is called vertical. The equation of an ellipse is in general form if it is in the form [latex]A{x}^{2}+B{y}^{2}+Cx+Dy+E=0[/latex], where A and B are either both positive or both negative. To convert the equation from general to standard form, use the method of completing the square.

Example: Finding the Standard Form of an Ellipse

Put the equation [latex]9{x}^{2}+4{y}^{2}-36x+24y+36=0[/latex] into standard form and graph the resulting ellipse.

Show Solution

First subtract 36 from both sides of the equation:

[latex]9{x}^{2}+4{y}^{2}-36x+24y=-36[/latex].

 

Next group the x terms together and the y terms together, and factor out the common factor:

[latex]\begin{array}{ccc}\hfill \left(9{x}^{2}-36x\right)+\left(4{y}^{2}+24y\right)& =\hfill & -36\hfill \\ \hfill 9\left({x}^{2}-4x\right)+4\left({y}^{2}+6y\right)& =\hfill & -36.\hfill \end{array}[/latex]

 

We need to determine the constant that, when added inside each set of parentheses, results in a perfect square. In the first set of parentheses, take half the coefficient of x and square it. This gives [latex]{\left(\frac{-4}{2}\right)}^{2}=4[/latex]. In the second set of parentheses, take half the coefficient of y and square it. This gives [latex]{\left(\frac{6}{2}\right)}^{2}=9[/latex]. Add these inside each pair of parentheses. Since the first set of parentheses has a 9 in front, we are actually adding 36 to the left-hand side. Similarly, we are adding 36 to the second set as well. Therefore the equation becomes

[latex]\begin{array}{}\\ 9\left({x}^{2}-4x+4\right)+4\left({y}^{2}+6y+9\right)=-36+36+36\hfill \\ 9\left({x}^{2}-4x+4\right)+4\left({y}^{2}+6y+9\right)=36.\hfill \end{array}[/latex]

 

Now factor both sets of parentheses and divide by 36:

[latex]\begin{array}{}\\ \hfill 9{\left(x - 2\right)}^{2}+4{\left(y+3\right)}^{2}& =\hfill & 36\hfill \\ \hfill \frac{9{\left(x - 2\right)}^{2}}{36}+\frac{4{\left(y+3\right)}^{2}}{36}& =\hfill & 1\hfill \\ \hfill \frac{{\left(x - 2\right)}^{2}}{4}+\frac{{\left(y+3\right)}^{2}}{9}& =\hfill & 1.\hfill \end{array}[/latex]

 

The equation is now in standard form. Comparing this to the theorem equation gives [latex]h=2[/latex], [latex]k=-3[/latex], [latex]a=3[/latex], and [latex]b=2[/latex]. This is a vertical ellipse with center at [latex]\left(2,-3\right)[/latex], major axis 6, and minor axis 4. The graph of this ellipse appears as follows.

Figure 9. The ellipse in [link].

Watch the following video to see the worked solution to Example: Finding the Standard Form of an Ellipse.

For closed captioning, open the video on its original page by clicking the Youtube logo in the lower right-hand corner of the video display. In YouTube, the video will begin at the same starting point as this clip, but will continue playing until the very end.

You can view the transcript for this segmented clip of “7.5 Conic Sections” here (opens in new window).

try it

Put the equation [latex]9{x}^{2}+16{y}^{2}+18x - 64y - 71=0[/latex] into standard form and graph the resulting ellipse.

Hint

Move the constant over and complete the square.

Show Solution

[latex]\frac{{\left(x+1\right)}^{2}}{16}+\frac{{\left(y - 2\right)}^{2}}{9}=1[/latex]

Figure 10.

According to Kepler’s first law of planetary motion, the orbit of a planet around the Sun is an ellipse with the Sun at one of the foci as shown in Figure 11 (a). Because Earth’s orbit is an ellipse, the distance from the Sun varies throughout the year. A commonly held misconception is that Earth is closer to the Sun in the summer. In fact, in summer for the northern hemisphere, Earth is farther from the Sun than during winter. The difference in season is caused by the tilt of Earth’s axis in the orbital plane. Comets that orbit the Sun, such as Halley’s Comet, also have elliptical orbits, as do moons orbiting the planets and satellites orbiting Earth.

Ellipses also have interesting reflective properties: A light ray emanating from one focus passes through the other focus after mirror reflection in the ellipse. The same thing occurs with a sound wave as well. The National Statuary Hall in the U.S. Capitol in Washington, DC, is a famous room in an elliptical shape as shown in Figure 11 (b). This hall served as the meeting place for the U.S. House of Representatives for almost fifty years. The location of the two foci of this semi-elliptical room are clearly identified by marks on the floor, and even if the room is full of visitors, when two people stand on these spots and speak to each other, they can hear each other much more clearly than they can hear someone standing close by. Legend has it that John Quincy Adams had his desk located on one of the foci and was able to eavesdrop on everyone else in the House without ever needing to stand. Although this makes a good story, it is unlikely to be true, because the original ceiling produced so many echoes that the entire room had to be hung with carpets to dampen the noise. The ceiling was rebuilt in 1902 and only then did the now-famous whispering effect emerge. Another famous whispering gallery—the site of many marriage proposals—is in Grand Central Station in New York City.

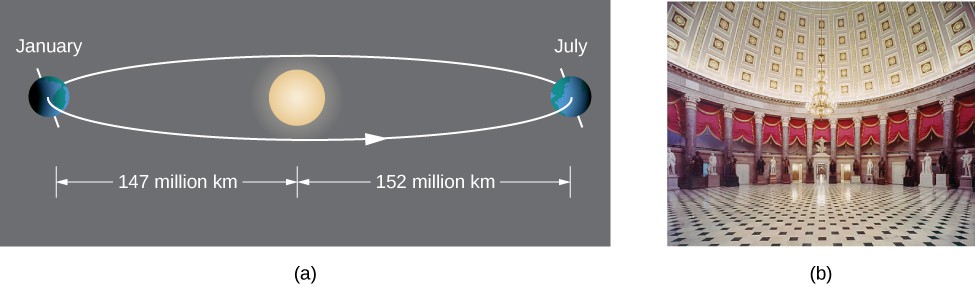
Figure 11. (a) Earth’s orbit around the Sun is an ellipse with the Sun at one focus. (b) Statuary Hall in the U.S. Capitol is a whispering gallery with an elliptical cross section.

Try It

Hyperbolas

A hyperbola can also be defined in terms of distances. In the case of a hyperbola, there are two foci and two directrices. Hyperbolas also have two asymptotes.

Definition

---

A hyperbola is the set of all points where the difference between their distances from two fixed points (the foci) is constant.

A graph of a typical hyperbola appears as follows.

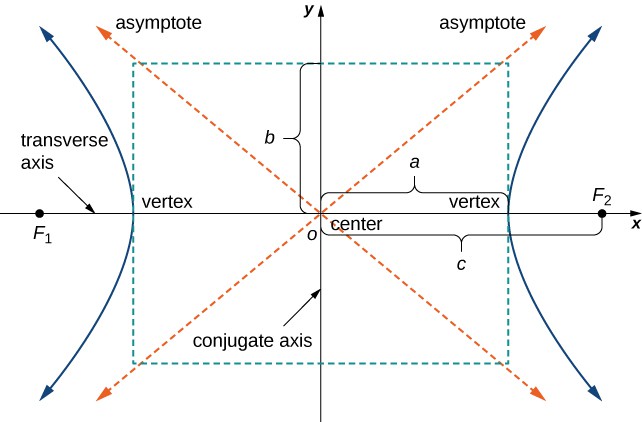
Figure 12. A typical hyperbola in which the difference of the distances from any point on the ellipse to the foci is constant. The transverse axis is also called the major axis, and the conjugate axis is also called the minor axis.

The derivation of the equation of a hyperbola in standard form is virtually identical to that of an ellipse. One slight hitch lies in the definition: The difference between two numbers is always positive. Let P be a point on the hyperbola with coordinates [latex]\left(x,y\right)[/latex]. Then the definition of the hyperbola gives [latex]|d\left(P,{F}_{1}\right)-d\left(P,{F}_{2}\right)|=\text{constant}[/latex]. To simplify the derivation, assume that P is on the right branch of the hyperbola, so the absolute value bars drop. If it is on the left branch, then the subtraction is reversed. The vertex of the right branch has coordinates [latex]\left(a,0\right)[/latex], so

[latex]d\left(P,{F}_{1}\right)-d\left(P,{F}_{2}\right)=\left(c+a\right)-\left(c-a\right)=2a[/latex].

 

This equation is therefore true for any point on the hyperbola. Returning to the coordinates [latex]\left(x,y\right)[/latex] for P:

[latex]\begin{array}{ccc}\hfill d\left(P,{F}_{1}\right)-d\left(P,{F}_{2}\right)& =\hfill & 2a\hfill \\ \hfill \sqrt{{\left(x+c\right)}^{2}+{y}^{2}}-\sqrt{{\left(x-c\right)}^{2}+{y}^{2}}& =\hfill & 2a.\hfill \end{array}[/latex]

 

Add the second radical from both sides and square both sides:

[latex]\begin{array}{ccc}\hfill \sqrt{{\left(x-c\right)}^{2}+{y}^{2}}& =\hfill & 2a+\sqrt{{\left(x+c\right)}^{2}+{y}^{2}}\hfill \\ \hfill {\left(x-c\right)}^{2}+{y}^{2}& =\hfill & 4{a}^{2}+4a\sqrt{{\left(x+c\right)}^{2}+{y}^{2}}+{\left(x+c\right)}^{2}+{y}^{2}\hfill \\ \hfill {x}^{2}-2cx+{c}^{2}+{y}^{2}& =\hfill & 4{a}^{2}+4a\sqrt{{\left(x+c\right)}^{2}+{y}^{2}}+{x}^{2}+2cx+{c}^{2}+{y}^{2}\hfill \\ \hfill -2cx& =\hfill & 4{a}^{2}+4a\sqrt{{\left(x+c\right)}^{2}+{y}^{2}}+2cx.\hfill \end{array}[/latex]

 

Now isolate the radical on the right-hand side and square again:

[latex]\begin{array}{ccc}\hfill -2cx& =\hfill & 4{a}^{2}+4a\sqrt{{\left(x+c\right)}^{2}+{y}^{2}}+2cx\hfill \\ \hfill 4a\sqrt{{\left(x+c\right)}^{2}+{y}^{2}}& =\hfill & -4{a}^{2}-4cx\hfill \\ \hfill \sqrt{{\left(x+c\right)}^{2}+{y}^{2}}& =\hfill & -a-\frac{cx}{a}\hfill \\ \hfill {\left(x+c\right)}^{2}+{y}^{2}& =\hfill & {a}^{2}+2cx+\frac{{c}^{2}{x}^{2}}{{a}^{2}}\hfill \\ \hfill {x}^{2}+2cx+{c}^{2}+{y}^{2}& =\hfill & {a}^{2}+2cx+\frac{{c}^{2}{x}^{2}}{{a}^{2}}\hfill \\ \hfill {x}^{2}+{c}^{2}+{y}^{2}& =\hfill & {a}^{2}+\frac{{c}^{2}{x}^{2}}{{a}^{2}}.\hfill \end{array}[/latex]

 

Isolate the variables on the left-hand side of the equation and the constants on the right-hand side:

[latex]\begin{array}{}\\ \hfill {x}^{2}-\frac{{c}^{2}{x}^{2}}{{a}^{2}}+{y}^{2}& =\hfill & {a}^{2}-{c}^{2}\hfill \\ \hfill \frac{\left({a}^{2}-{c}^{2}\right){x}^{2}}{{a}^{2}}+{y}^{2}& =\hfill & {a}^{2}-{c}^{2}.\hfill \end{array}[/latex]

 

Finally, divide both sides by [latex]{a}^{2}-{c}^{2}[/latex]. This gives the equation

[latex]\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{a}^{2}-{c}^{2}}=1[/latex].

 

We now define b so that [latex]{b}^{2}={c}^{2}-{a}^{2}[/latex]. This is possible because [latex]c>a[/latex]. Therefore the equation of the ellipse becomes

[latex]\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1[/latex].

 

Finally, if the center of the hyperbola is moved from the origin to the point [latex]\left(h,k\right)[/latex], we have the following standard form of a hyperbola.

theorem: Equation of a Hyperbola in Standard Form

---

Consider the hyperbola with center [latex]\left(h,k\right)[/latex], a horizontal major axis, and a vertical minor axis. Then the equation of this ellipse is

[latex]\frac{{\left(x-h\right)}^{2}}{{a}^{2}}-\frac{{\left(y-k\right)}^{2}}{{b}^{2}}=1[/latex]

 

and the foci are located at [latex]\left(h\pm c,k\right)[/latex], where [latex]{c}^{2}={a}^{2}+{b}^{2}[/latex]. The equations of the asymptotes are given by [latex]y=k\pm \frac{b}{a}\left(x-h\right)[/latex]. The equations of the directrices are

[latex]x=k\pm \frac{{a}^{2}}{\sqrt{{a}^{2}+{b}^{2}}}=h\pm \frac{{a}^{2}}{c}[/latex].

 

If the major axis is vertical, then the equation of the hyperbola becomes

[latex]\frac{{\left(y-k\right)}^{2}}{{a}^{2}}-\frac{{\left(x-h\right)}^{2}}{{b}^{2}}=1[/latex]

 

and the foci are located at [latex]\left(h,k\pm c\right)[/latex], where [latex]{c}^{2}={a}^{2}+{b}^{2}[/latex]. The equations of the asymptotes are given by [latex]y=k\pm \frac{a}{b}\left(x-h\right)[/latex]. The equations of the directrices are

[latex]y=k\pm \frac{{a}^{2}}{\sqrt{{a}^{2}+{b}^{2}}}=k\pm \frac{{a}^{2}}{c}[/latex].

 

If the major axis (transverse axis) is horizontal, then the hyperbola is called horizontal, and if the major axis is vertical then the hyperbola is called vertical. The equation of a hyperbola is in general form if it is in the form [latex]A{x}^{2}+B{y}^{2}+Cx+Dy+E=0[/latex], where [latex]A[/latex] and [latex]B[/latex] have opposite signs. In order to convert the equation from general to standard form, use the method of completing the square.

Example: Finding the Standard Form of a Hyperbola

Put the equation [latex]9{x}^{2}-16{y}^{2}+36x+32y - 124=0[/latex] into standard form and graph the resulting hyperbola. What are the equations of the asymptotes?

Show Solution

First add [latex]124[/latex] to both sides of the equation:

[latex]9{x}^{2}-16{y}^{2}+36x+32y=124[/latex].

 

Next group the x terms together and the y terms together, then factor out the common factors:

[latex]\begin{array}{ccc}\hfill \left(9{x}^{2}+36x\right)-\left(16{y}^{2}-32y\right)& =\hfill & 124\hfill \\ \hfill 9\left({x}^{2}+4x\right)-16\left({y}^{2}-2y\right)& =\hfill & 124.\hfill \end{array}[/latex]

 

We need to determine the constant that, when added inside each set of parentheses, results in a perfect square. In the first set of parentheses, take half the coefficient of [latex]x[/latex] and square it. This gives [latex]{\left(\frac{4}{2}\right)}^{2}=4[/latex]. In the second set of parentheses, take half the coefficient of y and square it. This gives [latex]{\left(\frac{-2}{2}\right)}^{2}=1[/latex]. Add these inside each pair of parentheses. Since the first set of parentheses has a 9 in front, we are actually adding 36 to the left-hand side. Similarly, we are subtracting 16 from the second set of parentheses. Therefore the equation becomes

[latex]\begin{array}{}\\ 9\left({x}^{2}+4x+4\right)-16\left({y}^{2}-2y+1\right)=124+36 - 16\hfill \\ 9\left({x}^{2}+4x+4\right)-16\left({y}^{2}-2y+1\right)=144.\hfill \end{array}[/latex]

 

Next factor both sets of parentheses and divide by 144:

[latex]\begin{array}{}\\ \hfill 9{\left(x+2\right)}^{2}-16{\left(y - 1\right)}^{2}& =\hfill & 144\hfill \\ \hfill \frac{9{\left(x+2\right)}^{2}}{144}-\frac{16{\left(y - 1\right)}^{2}}{144}& =\hfill & 1\hfill \\ \hfill \frac{{\left(x+2\right)}^{2}}{16}-\frac{{\left(y - 1\right)}^{2}}{9}& =\hfill & 1.\hfill \end{array}[/latex]

 

The equation is now in standard form. Comparing this to the theorem gives [latex]h=-2[/latex], [latex]k=1[/latex], [latex]a=4[/latex], and [latex]b=3[/latex]. This is a horizontal hyperbola with center at [latex]\left(-2,1\right)[/latex] and asymptotes given by the equations [latex]y=1\pm \frac{3}{4}\left(x+2\right)[/latex]. The graph of this hyperbola appears in the following figure.

Figure 13. Graph of the hyperbola in [link].

Watch the following video to see the worked solution to Example: Finding the Standard Form of a Hyperbola.

For closed captioning, open the video on its original page by clicking the Youtube logo in the lower right-hand corner of the video display. In YouTube, the video will begin at the same starting point as this clip, but will continue playing until the very end.

You can view the transcript for this segmented clip of “7.5 Conic Sections” here (opens in new window).

try it

Put the equation [latex]4{y}^{2}-9{x}^{2}+16y+18x - 29=0[/latex] into standard form and graph the resulting hyperbola. What are the equations of the asymptotes?

Hint

Move the constant over and complete the square. Check which direction the hyperbola opens.

Show Solution

[latex]\frac{{\left(y+2\right)}^{2}}{9}-\frac{{\left(x - 1\right)}^{2}}{4}=1[/latex]. This is a vertical hyperbola. Asymptotes [latex]y=-2\pm \frac{3}{2}\left(x - 1\right)[/latex].

Figure 14.

Hyperbolas also have interesting reflective properties. A ray directed toward one focus of a hyperbola is reflected by a hyperbolic mirror toward the other focus. This concept is illustrated in the following figure.

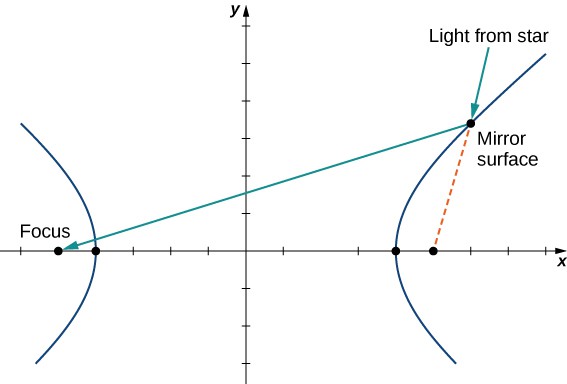
Figure 15. A hyperbolic mirror used to collect light from distant stars.

This property of the hyperbola has important applications. It is used in radio direction finding (since the difference in signals from two towers is constant along hyperbolas), and in the construction of mirrors inside telescopes (to reflect light coming from the parabolic mirror to the eyepiece). Another interesting fact about hyperbolas is that for a comet entering the solar system, if the speed is great enough to escape the Sun’s gravitational pull, then the path that the comet takes as it passes through the solar system is hyperbolic.

Try It