Learning Outcomes
- Use the sum of rectangular areas to approximate the area under a curve
Now that we have the necessary notation, we return to the problem at hand: approximating the area under a curve. Let [latex]f(x)[/latex] be a continuous, nonnegative function defined on the closed interval [latex][a,b][/latex]. We want to approximate the area [latex]A[/latex] bounded by [latex]f(x)[/latex] above, the [latex]x[/latex]-axis below, the line [latex]x=a[/latex] on the left, and the line [latex]x=b[/latex] on the right (Figure 1).
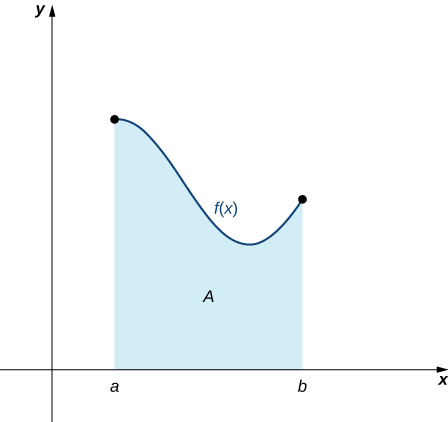
Figure 1. An area (shaded region) bounded by the curve [latex]f(x)[/latex] at top, the x-axis at bottom, the line [latex]x=a[/latex] to the left, and the line [latex]x=b[/latex] at right.
How do we approximate the area under this curve? The approach is a geometric one. By dividing a region into many small shapes that have known area formulas, we can sum these areas and obtain a reasonable estimate of the true area. We begin by dividing the interval [latex][a,b][/latex] into [latex]n[/latex] subintervals of equal width, [latex]\frac{b-a}{n}[/latex]. We do this by selecting equally spaced points [latex]x_0,x_1,x_2,\cdots,x_n[/latex] with [latex]x_0=a, \, x_n=b[/latex], and
for [latex]i=1,2,3,\cdots,n[/latex].
We denote the width of each subinterval with the notation [latex]\Delta x[/latex], so [latex]\Delta x=\dfrac{b-a}{n}[/latex] and
for [latex]i=1,2,3,\cdots,n[/latex]. This notion of dividing an interval [latex][a,b][/latex] into subintervals by selecting points from within the interval is used quite often in approximating the area under a curve, so let’s define some relevant terminology.
Definition
A set of points [latex]P=\{x_i\}[/latex] for [latex]i=0,1,2,\cdots,n[/latex] with [latex]a=x_0<x_1<x_2<\cdots<x_n=b[/latex], which divides the interval [latex][a,b][/latex] into subintervals of the form [latex][x_0,x_1], \, [x_1,x_2],\cdots,[x_{n-1},x_n][/latex] is called a partition of [latex][a,b][/latex]. If the subintervals all have the same width, the set of points forms a regular partition of the interval [latex][a,b][/latex].
We can use this regular partition as the basis of a method for estimating the area under the curve. We next examine two methods: the left-endpoint approximation and the right-endpoint approximation.
Left-Endpoint Approximation
On each subinterval [latex][x_{i-1},x_i][/latex] (for [latex]i=1,2,3,\cdots,n[/latex]), construct a rectangle with width [latex]\Delta x[/latex] and height equal to [latex]f(x_{i-1})[/latex], which is the function value at the left endpoint of the subinterval. Then the area of this rectangle is [latex]f(x_{i-1})\Delta x[/latex]. Adding the areas of all these rectangles, we get an approximate value for [latex]A[/latex] (Figure 2). We use the notation [latex]L_n[/latex] to denote that this is a left-endpoint approximation of [latex]A[/latex] using [latex]n[/latex] subintervals.
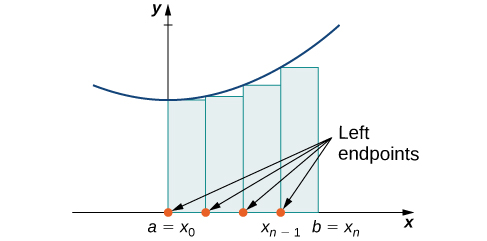
Figure 2. In the left-endpoint approximation of area under a curve, the height of each rectangle is determined by the function value at the left of each subinterval.
The second method for approximating area under a curve is the right-endpoint approximation. It is almost the same as the left-endpoint approximation, but now the heights of the rectangles are determined by the function values at the right of each subinterval.
Right-Endpoint Approximation
Construct a rectangle on each subinterval [latex][x_{i-1},x_i][/latex], only this time the height of the rectangle is determined by the function value [latex]f(x_i)[/latex] at the right endpoint of the subinterval. Then, the area of each rectangle is [latex]f(x_i)\Delta x[/latex] and the approximation for [latex]A[/latex] is given by
The notation [latex]R_n[/latex] indicates this is a right-endpoint approximation for [latex]A[/latex] (Figure 3).
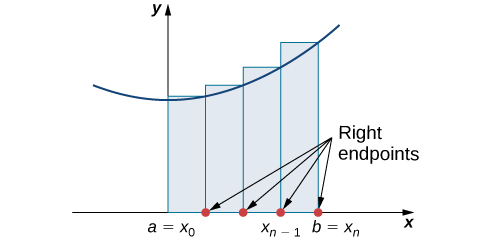
Figure 3. In the right-endpoint approximation of area under a curve, the height of each rectangle is determined by the function value at the right of each subinterval. Note that the right-endpoint approximation differs from the left-endpoint approximation in (Figure).
The graphs in Figure 4 represent the curve [latex]f(x)=\frac{x^2}{2}[/latex]. In graph (a) we divide the region represented by the interval [latex][0,3][/latex] into six subintervals, each of width 0.5. Thus, [latex]\Delta x=0.5[/latex]. We then form six rectangles by drawing vertical lines perpendicular to [latex]x_{i-1}[/latex], the left endpoint of each subinterval. We determine the height of each rectangle by calculating [latex]f(x_{i-1})[/latex] for [latex]i=1,2,3,4,5,6[/latex]. The intervals are [latex][0,0.5], \, [0.5,1], \, [1,1.5], \, [1.5,2], \, [2,2.5], \, [2.5,3][/latex]. We find the area of each rectangle by multiplying the height by the width. Then, the sum of the rectangular areas approximates the area between [latex]f(x)[/latex] and the [latex]x[/latex]-axis. When the left endpoints are used to calculate height, we have a left-endpoint approximation. Thus,
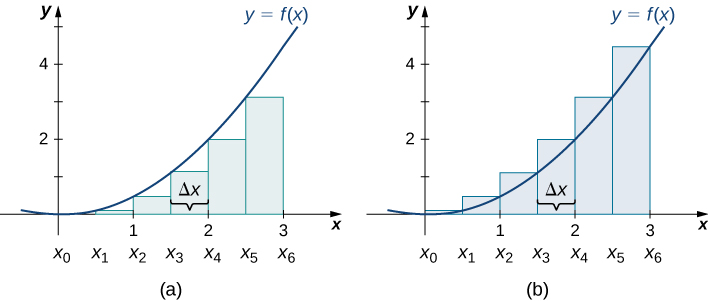
Figure 4. Methods of approximating the area under a curve by using (a) the left endpoints and (b) the right endpoints.
In Figure 4(b), we draw vertical lines perpendicular to [latex]x_i[/latex] such that [latex]x_i[/latex] is the right endpoint of each subinterval, and calculate [latex]f(x_i)[/latex] for [latex]i=1,2,3,4,5,6[/latex]. We multiply each [latex]f(x_i)[/latex] by [latex]\Delta x[/latex] to find the rectangular areas, and then add them. This is a right-endpoint approximation of the area under [latex]f(x)[/latex]. Thus,
Example: Approximating the Area Under a Curve
Use both left-endpoint and right-endpoint approximations to approximate the area under the curve of [latex]f(x)=x^2[/latex] on the interval [latex][0,2][/latex]; use [latex]n=4[/latex].
Watch the following video to see the worked solution to Example: Approximating the Area Under a Curve.
Try It
Sketch left-endpoint and right-endpoint approximations for [latex]f(x)=\frac{1}{x}[/latex] on [latex][1,2][/latex]; use [latex]n=4[/latex]. Approximate the area using both methods.
Looking at Figure 4 and the graphs in the previous example, we can see that when we use a small number of intervals, neither the left-endpoint approximation nor the right-endpoint approximation is a particularly accurate estimate of the area under the curve. However, it seems logical that if we increase the number of points in our partition, our estimate of [latex]A[/latex] will improve. We will have more rectangles, but each rectangle will be thinner, so we will be able to fit the rectangles to the curve more precisely.
We can demonstrate the improved approximation obtained through smaller intervals with an example. Let’s explore the idea of increasing [latex]n[/latex], first in a left-endpoint approximation with four rectangles, then eight rectangles, and finally 32 rectangles. Then, let’s do the same thing in a right-endpoint approximation, using the same sets of intervals, of the same curved region. Figure 7 shows the area of the region under the curve [latex]f(x)=(x-1)^3+4[/latex] on the interval [latex][0,2][/latex] using a left-endpoint approximation where [latex]n=4[/latex]. The width of each rectangle is
The area is approximated by the summed areas of the rectangles, or
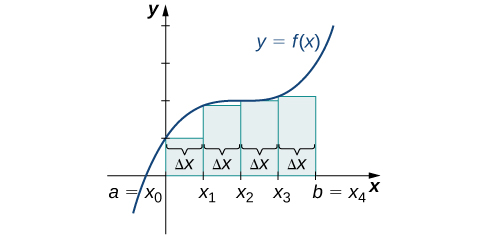
Figure 8. With a left-endpoint approximation and dividing the region from a to b into four equal intervals, the area under the curve is approximately equal to the sum of the areas of the rectangles.
Figure 9 shows the same curve divided into eight subintervals. Comparing the graph with four rectangles in Figure 8 with this graph with eight rectangles, we can see there appears to be less white space under the curve when [latex]n=8[/latex]. This white space is area under the curve we are unable to include using our approximation. The area of the rectangles is
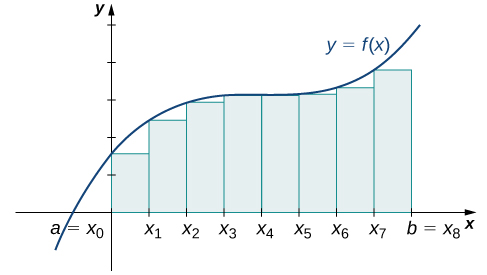
Figure 9. The region under the curve is divided into [latex]n=8[/latex] rectangular areas of equal width for a left-endpoint approximation.
The graph in Figure 10 shows the same function with 32 rectangles inscribed under the curve. There appears to be little white space left. The area occupied by the rectangles is
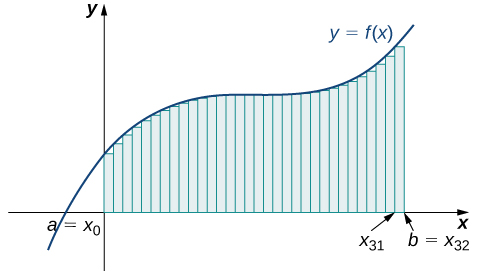
Figure 10. Here, 32 rectangles are inscribed under the curve for a left-endpoint approximation.
We can carry out a similar process for the right-endpoint approximation method. A right-endpoint approximation of the same curve, using four rectangles (Figure 11), yields an area
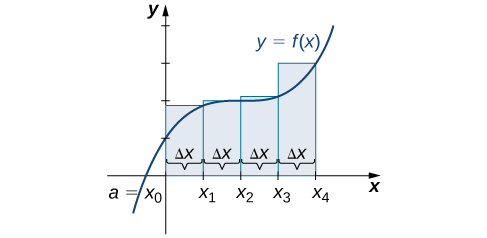
Figure 11. Now we divide the area under the curve into four equal subintervals for a right-endpoint approximation.
Dividing the region over the interval [latex][0,2][/latex] into eight rectangles results in [latex]\Delta x=\frac{2-0}{8}=0.25[/latex]. The graph is shown in Figure 12. The area is
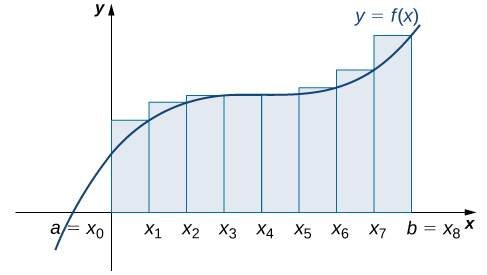
Figure 12. Here we use right-endpoint approximation for a region divided into eight equal subintervals.
Last, the right-endpoint approximation with [latex]n=32[/latex] is close to the actual area (Figure 13). The area is approximately
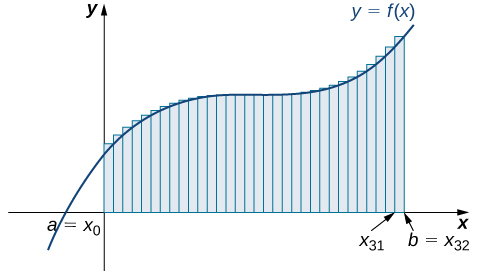
Figure 13. The region is divided into 32 equal subintervals for a right-endpoint approximation.
Based on these figures and calculations, it appears we are on the right track; the rectangles appear to approximate the area under the curve better as [latex]n[/latex] gets larger. Furthermore, as [latex]n[/latex] increases, both the left-endpoint and right-endpoint approximations appear to approach an area of 8 square units. The table below shows a numerical comparison of the left- and right-endpoint methods. The idea that the approximations of the area under the curve get better and better as [latex]n[/latex] gets larger and larger is very important, and we now explore this idea in more detail.
| Values of [latex]n[/latex] | Approximate Area [latex]L_n[/latex] | Approximate Area [latex]R_n[/latex] |
|---|---|---|
| [latex]n=4[/latex] | 7.5 | 8.5 |
| [latex]n=8[/latex] | 7.75 | 8.25 |
| [latex]n=32[/latex] | 7.94 | 8.06 |



