Bounded Sequences

Learning Outcomes

Determine the convergence or divergence of a given sequence

We now turn our attention to one of the most important theorems involving sequences: the Monotone Convergence Theorem. Before stating the theorem, we need to introduce some terminology and motivation. We begin by defining what it means for a sequence to be bounded.

Definition

A sequence [latex]\left\{{a}_{n}\right\}[/latex] is bounded above if there exists a real number [latex]M[/latex] such that

[latex]{a}_{n}\le M[/latex]

for all positive integers [latex]n[/latex].

A sequence [latex]\left\{{a}_{n}\right\}[/latex] is bounded below if there exists a real number [latex]M[/latex] such that

[latex]M\le {a}_{n}[/latex]

for all positive integers [latex]n[/latex].

A sequence [latex]\left\{{a}_{n}\right\}[/latex] is a bounded sequence if it is bounded above and bounded below.

If a sequence is not bounded, it is an unbounded sequence.

For example, the sequence [latex]\left\{\frac{1}{n}\right\}[/latex] is bounded above because [latex]\frac{1}{n}\le 1[/latex] for all positive integers [latex]n[/latex]. It is also bounded below because [latex]\frac{1}{n}\ge 0[/latex] for all positive integers n. Therefore, [latex]\left\{\frac{1}{n}\right\}[/latex] is a bounded sequence. On the other hand, consider the sequence [latex]\left\{{2}^{n}\right\}[/latex]. Because [latex]{2}^{n}\ge 2[/latex] for all [latex]n\ge 1[/latex], the sequence is bounded below. However, the sequence is not bounded above. Therefore, [latex]\left\{{2}^{n}\right\}[/latex] is an unbounded sequence.

We now discuss the relationship between boundedness and convergence. Suppose a sequence [latex]\left\{{a}_{n}\right\}[/latex] is unbounded. Then it is not bounded above, or not bounded below, or both. In either case, there are terms [latex]{a}_{n}[/latex] that are arbitrarily large in magnitude as [latex]n[/latex] gets larger. As a result, the sequence [latex]\left\{{a}_{n}\right\}[/latex] cannot converge. Therefore, being bounded is a necessary condition for a sequence to converge.

Theorem: Convergent Sequences Are Bounded

If a sequence [latex]\left\{{a}_{n}\right\}[/latex] converges, then it is bounded.

Note that a sequence being bounded is not a sufficient condition for a sequence to converge. For example, the sequence [latex]\left\{{\left(-1\right)}^{n}\right\}[/latex] is bounded, but the sequence diverges because the sequence oscillates between [latex]1[/latex] and [latex]-1[/latex] and never approaches a finite number. We now discuss a sufficient (but not necessary) condition for a bounded sequence to converge.

Consider a bounded sequence [latex]\left\{{a}_{n}\right\}[/latex]. Suppose the sequence [latex]\left\{{a}_{n}\right\}[/latex] is increasing. That is, [latex]{a}_{1}\le {a}_{2}\le {a}_{3}\ldots[/latex]. Since the sequence is increasing, the terms are not oscillating. Therefore, there are two possibilities. The sequence could diverge to infinity, or it could converge. However, since the sequence is bounded, it is bounded above and the sequence cannot diverge to infinity. We conclude that [latex]\left\{{a}_{n}\right\}[/latex] converges. For example, consider the sequence

[latex]\left\{\frac{1}{2},\frac{2}{3},\frac{3}{4},\frac{4}{5}\text{,}\ldots\right\}[/latex].

Since this sequence is increasing and bounded above, it converges. Next, consider the sequence

[latex]\left\{2,0,3,0,4,0,1,-\frac{1}{2},-\frac{1}{3},-\frac{1}{4}\text{,}\ldots\right\}[/latex].

Even though the sequence is not increasing for all values of [latex]n[/latex], we see that [latex]-\frac{1}{2}<\text{-}\frac{1}{3}<\text{-}\frac{1}{4}<\cdots[/latex]. Therefore, starting with the eighth term, [latex]{a}_{8}=-\frac{1}{2}[/latex], the sequence is increasing. In this case, we say the sequence is eventually increasing. Since the sequence is bounded above, it converges. It is also true that if a sequence is decreasing (or eventually decreasing) and bounded below, it also converges.

Definition

A sequence [latex]\left\{{a}_{n}\right\}[/latex] is increasing for all [latex]n\ge {n}_{0}[/latex] if

[latex]{a}_{n}\le {a}_{n+1}\text{ for all }n\ge {n}_{0}[/latex].

A sequence [latex]\left\{{a}_{n}\right\}[/latex] is decreasing for all [latex]n\ge {n}_{0}[/latex] if

[latex]{a}_{n}\ge {a}_{n+1}\text{ for all }n\ge {n}_{0}[/latex].

A sequence [latex]\left\{{a}_{n}\right\}[/latex] is a monotone sequence for all [latex]n\ge {n}_{0}[/latex] if it is increasing for all [latex]n\ge {n}_{0}[/latex] or decreasing for all [latex]n\ge {n}_{0}[/latex].

We now have the necessary definitions to state the Monotone Convergence Theorem, which gives a sufficient condition for convergence of a sequence.

Theorem: Monotone Convergence Theorem

If [latex]\left\{{a}_{n}\right\}[/latex] is a bounded sequence and there exists a positive integer [latex]{n}_{0}[/latex] such that [latex]\left\{{a}_{n}\right\}[/latex] is monotone for all [latex]n\ge {n}_{0}[/latex], then [latex]\left\{{a}_{n}\right\}[/latex] converges.

The proof of this theorem is beyond the scope of this text. Instead, we provide a graph to show intuitively why this theorem makes sense (Figure 6).

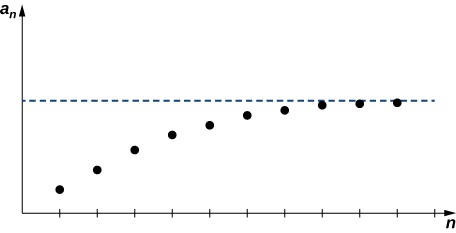
A graph in quadrant 1 with the x and y axes labeled n and a_n, respectively. A dotted horizontal is drawn from the a_n axis into quadrant 1. Many points are plotted under the dotted line, increasing in a_n value and converging to the dotted line.

In the following example, we show how the Monotone Convergence Theorem can be used to prove convergence of a sequence.

Example: Using the Monotone Convergence Theorem

For each of the following sequences, use the Monotone Convergence Theorem to show the sequence converges and find its limit.

[latex]\left\{\frac{{4}^{n}}{n\text{!}}\right\}[/latex]
[latex]\left\{{a}_{n}\right\}[/latex] defined recursively such that

[latex]{a}_{1}=2\text{ and }{a}_{n+1}=\frac{{a}_{n}}{2}+\frac{1}{2{a}_{n}}\text{ for all }n\ge 2[/latex].

Show Solution

Writing out the first few terms, we see that

[latex]\left\{\frac{{4}^{n}}{n\text{!}}\right\}=\left\{4,8,\frac{32}{3},\frac{32}{3},\frac{128}{15}\text{,}\ldots\right\}[/latex].

At first, the terms increase. However, after the third term, the terms decrease. In fact, the terms decrease for all [latex]n\ge 3[/latex]. We can show this as follows.

[latex]{a}_{n+1}=\frac{{4}^{n+1}}{\left(n+1\right)\text{!}}=\frac{4}{n+1}\cdot \frac{{4}^{n}}{n\text{!}}=\frac{4}{n+1}\cdot {a}_{n}\le {a}_{n}\text{ if }n\ge 3[/latex].

Therefore, the sequence is decreasing for all [latex]n\ge 3[/latex]. Further, the sequence is bounded below by [latex]0[/latex] because [latex]\frac{{4}^{n}}{n\text{!}}\ge 0[/latex] for all positive integers [latex]n[/latex]. Therefore, by the Monotone Convergence Theorem, the sequence converges.

To find the limit, we use the fact that the sequence converges and let [latex]L=\underset{n\to \infty }{\text{lim}}{a}_{n}[/latex]. Now note this important observation. Consider [latex]\underset{n\to \infty }{\text{lim}}{a}_{n+1}[/latex]. Since

[latex]\left\{{a}_{n+1}\right\}=\left\{{a}_{2,}{a}_{3},{a}_{4}\text{,}\ldots\right\}[/latex],

the only difference between the sequences [latex]\left\{{a}_{n+1}\right\}[/latex] and [latex]\left\{{a}_{n}\right\}[/latex] is that [latex]\left\{{a}_{n+1}\right\}[/latex] omits the first term. Since a finite number of terms does not affect the convergence of a sequence,

[latex]\underset{n\to \infty }{\text{lim}}{a}_{n+1}=\underset{n\to \infty }{\text{lim}}{a}_{n}=L[/latex].

Combining this fact with the equation

[latex]{a}_{n+1}=\frac{4}{n+1}{a}_{n}[/latex]

and taking the limit of both sides of the equation

[latex]\underset{n\to \infty }{\text{lim}}{a}_{n+1}=\underset{n\to \infty }{\text{lim}}\frac{4}{n+1}{a}_{n}[/latex],

we can conclude that

[latex]L=0\cdot L=0[/latex].
Writing out the first several terms,

[latex]\left\{2,\frac{5}{4},\frac{41}{40},\frac{3281}{3280}\text{,}\ldots\right\}[/latex].

we can conjecture that the sequence is decreasing and bounded below by [latex]1[/latex]. To show that the sequence is bounded below by [latex]1[/latex], we can show that

[latex]\frac{{a}_{n}}{2}+\frac{1}{2{a}_{n}}\ge 1[/latex].

To show this, first rewrite

[latex]\frac{{a}_{n}}{2}+\frac{1}{2{a}_{n}}=\frac{{a}_{n}^{2}+1}{2{a}_{n}}[/latex].

Since [latex]{a}_{1}>0[/latex] and [latex]{a}_{2}[/latex] is defined as a sum of positive terms, [latex]{a}_{2}>0[/latex]. Similarly, all terms [latex]{a}_{n}>0[/latex]. Therefore,

[latex]\frac{{a}_{n}^{2}+1}{2{a}_{n}}\ge 1[/latex]

if and only if

[latex]{a}_{n}^{2}+1\ge 2{a}_{n}[/latex].

Rewriting the inequality [latex]{a}_{n}^{2}+1\ge 2{a}_{n}[/latex] as [latex]{a}_{n}^{2}-2{a}_{n}+1\ge 0[/latex], and using the fact that

[latex]{a}_{n}^{2}-2{a}_{n}+1={\left({a}_{n}-1\right)}^{2}\ge 0[/latex]

because the square of any real number is nonnegative, we can conclude that

[latex]\frac{{a}_{n}}{2}+\frac{1}{2{a}_{n}}\ge 1[/latex].

To show that the sequence is decreasing, we must show that [latex]{a}_{n+1}\le {a}_{n}[/latex] for all [latex]n\ge 1[/latex]. Since [latex]1\le {a}_{n}^{2}[/latex], it follows that

[latex]{a}_{n}^{2}+1\le 2{a}_{n}^{2}[/latex].

Dividing both sides by [latex]2{a}_{n}[/latex], we obtain

[latex]\frac{{a}_{n}}{2}+\frac{1}{2{a}_{n}}\le {a}_{n}[/latex].

Using the definition of [latex]{a}_{n+1}[/latex], we conclude that

[latex]{a}_{n+1}=\frac{{a}_{n}}{2}+\frac{1}{2{a}_{n}}\le {a}_{n}[/latex].

Since [latex]\left\{{a}_{n}\right\}[/latex] is bounded below and decreasing, by the Monotone Convergence Theorem, it converges.

To find the limit, let [latex]L=\underset{n\to \infty }{\text{lim}}{a}_{n}[/latex]. Then using the recurrence relation and the fact that [latex]\underset{n\to \infty }{\text{lim}}{a}_{n}=\underset{n\to \infty }{\text{lim}}{a}_{n+1}[/latex], we have

[latex]\underset{n\to \infty }{\text{lim}}{a}_{n+1}=\underset{n\to \infty }{\text{lim}}\left(\frac{{a}_{n}}{2}+\frac{1}{2{a}_{n}}\right)[/latex],

and therefore

[latex]L=\frac{L}{2}+\frac{1}{2L}[/latex].

Multiplying both sides of this equation by [latex]2L[/latex], we arrive at the equation

[latex]2{L}^{2}={L}^{2}+1[/latex].

Solving this equation for [latex]L[/latex], we conclude that [latex]{L}^{2}=1[/latex], which implies [latex]L=\pm 1[/latex]. Since all the terms are positive, the limit [latex]L=1[/latex].

try it

Consider the sequence [latex]\left\{{a}_{n}\right\}[/latex] defined recursively such that [latex]{a}_{1}=1[/latex], [latex]{a}_{n}=\frac{{a}_{n - 1}}{2}[/latex]. Use the Monotone Convergence Theorem to show that this sequence converges and find its limit.

Hint

Show Solution

Watch the following video to see the worked solution to the above Try IT.

For closed captioning, open the video on its original page by clicking the Youtube logo in the lower right-hand corner of the video display. In YouTube, the video will begin at the same starting point as this clip, but will continue playing until the very end.

You can view the transcript for this segmented clip of “5.1.3” here (opens in new window).

Try It

ACTIVITY: Fibonacci Numbers

The Fibonacci numbers are defined recursively by the sequence [latex]\left\{{F}_{n}\right\}[/latex] where [latex]{F}_{0}=0[/latex], [latex]{F}_{1}=1[/latex] and for [latex]n\ge 2[/latex],

[latex]{F}_{n}={F}_{n - 1}+{F}_{n - 2}[/latex].

Here we look at properties of the Fibonacci numbers.

Write out the first twenty Fibonacci numbers.
Find a closed formula for the Fibonacci sequence by using the following steps.
1. Consider the recursively defined sequence [latex]\left\{{x}_{n}\right\}[/latex] where [latex]{x}_{o}=c[/latex] and [latex]{x}_{n+1}=a{x}_{n}[/latex]. Show that this sequence can be described by the closed formula [latex]{x}_{n}=c{a}^{n}[/latex] for all [latex]n\ge 0[/latex].
2. Using the result from part a. as motivation, look for a solution of the equation
  
  [latex]{F}_{n}={F}_{n - 1}+{F}_{n - 2}[/latex]
  
  of the form [latex]{F}_{n}=c{\lambda }^{n}[/latex]. Determine what two values for [latex]\lambda[/latex] will allow [latex]{F}_{n}[/latex] to satisfy this equation.
3. Consider the two solutions from part b.: [latex]{\lambda }_{1}[/latex] and [latex]{\lambda }_{2}[/latex]. Let [latex]{F}_{n}={c}_{1}{\lambda }_{1}{}^{n}+{c}_{2}{\lambda }_{2}{}^{n}[/latex]. Use the initial conditions [latex]{F}_{0}[/latex] and [latex]{F}_{1}[/latex] to determine the values for the constants [latex]{c}_{1}[/latex] and [latex]{c}_{2}[/latex] and write the closed formula [latex]{F}_{n}[/latex].
Use the answer in 2 c. to show that

[latex]\underset{n\to \infty }{\text{lim}}\frac{{F}_{n+1}}{{F}_{n}}=\frac{1+\sqrt{5}}{2}[/latex].

The number [latex]\varphi =\frac{\left(1+\sqrt{5}\right)}{2}[/latex] is known as the golden ratio (Figures 7 and 8).

Figure 7. The seeds in a sunflower exhibit spiral patterns curving to the left and to the right. The number of spirals in each direction is always a Fibonacci number—always. (credit: modification of work by Esdras Calderan, Wikimedia Commons)

Figure 8. The proportion of the golden ratio appears in many famous examples of art and architecture. The ancient Greek temple known as the Parthenon was designed with these proportions, and the ratio appears again in many of the smaller details. (credit: modification of work by TravelingOtter, Flickr)

Module 5: Sequences and Series

Learning Outcomes

Definition

Theorem: Convergent Sequences Are Bounded

Definition

Theorem: Monotone Convergence Theorem

Example: Using the Monotone Convergence Theorem

try it

Try It

ACTIVITY: Fibonacci Numbers

Candela Citations