Exponential Growth Model

Learning Outcomes

  • Use the exponential growth model in applications, including population growth and compound interest
  • Explain the concept of doubling time

Many systems exhibit exponential growth. These systems follow a model of the form [latex]y={y}_{0}{e}^{kt},[/latex] where [latex]{y}_{0}[/latex] represents the initial state of the system and [latex]k[/latex] is a positive constant, called the growth constant. Notice that in an exponential growth model, we have

[latex]{y}^{\prime }=k{y}_{0}{e}^{kt}=ky[/latex]

 

That is, the rate of growth is proportional to the current function value. This is a key feature of exponential growth. The equation above involves derivatives and is called a differential equation. We learn more about differential equations in Introduction to Differential Equations in the second volume of this text.

Exponential Growth Model

Systems that exhibit exponential growth increase according to the mathematical model

[latex]y={y}_{0}{e}^{kt},[/latex]

 

where [latex]{y}_{0}[/latex] represents the initial state of the system and [latex]k>0[/latex] is a constant, called the growth constant.

Population growth is a common example of exponential growth. Consider a population of bacteria, for instance. It seems plausible that the rate of population growth would be proportional to the size of the population. After all, the more bacteria there are to reproduce, the faster the population grows. Figure 1 and the table below represent the growth of a population of bacteria with an initial population of 200 bacteria and a growth constant of 0.02. Notice that after only 2 hours [latex](120[/latex] minutes), the population is 10 times its original size!

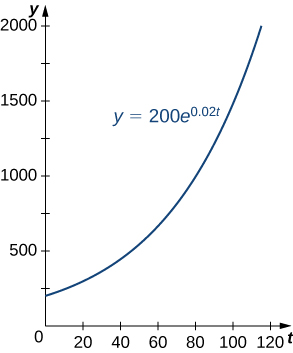
This figure is a graph. It is the exponential curve for y=200e^0.02t. It is in the first quadrant and an increasing function. It begins on the y-axis.

Figure 1. An example of exponential growth for bacteria.

Exponential Growth of a Bacterial Population
Time (min) Population Size (no. of bacteria)
10 244
20 298
30 364
40 445
50 544
60 664
70 811
80 991
90 1210
100 1478
110 1805
120 2205

Note that we are using a continuous function to model what is inherently discrete behavior. At any given time, the real-world population contains a whole number of bacteria, although the model takes on noninteger values. When using exponential growth models, we must always be careful to interpret the function values in the context of the phenomenon we are modeling.

Example: Population Growth

Consider the population of bacteria described earlier. This population grows according to the function [latex]f(t)=200{e}^{0.02t},[/latex] where [latex]t[/latex] is measured in minutes. How many bacteria are present in the population after 5 hours [latex](300[/latex] minutes)? When does the population reach 100,000 bacteria?

Try It

Consider a population of bacteria that grows according to the function [latex]f(t)=500{e}^{0.05t},[/latex] where [latex]t[/latex] is measured in minutes. How many bacteria are present in the population after 4 hours? When does the population reach 100 million bacteria?

Let’s now turn our attention to a financial application: compound interest. Interest that is not compounded is called simple interest. Simple interest is paid once, at the end of the specified time period (usually 1 year). So, if we put [latex]$1000[/latex] in a savings account earning 2% simple interest per year, then at the end of the year we have

[latex]1000(1+0.02)=$1020.[/latex]

 

Compound interest is paid multiple times per year, depending on the compounding period. Therefore, if the bank compounds the interest every 6 months, it credits half of the year’s interest to the account after 6 months. During the second half of the year, the account earns interest not only on the initial [latex]$1000,[/latex] but also on the interest earned during the first half of the year. Mathematically speaking, at the end of the year, we have

[latex]1000{(1+\frac{0.02}{2})}^{2}=$1020.10.[/latex]

 

Similarly, if the interest is compounded every 4 months, we have

[latex]1000{(1+\frac{0.02}{3})}^{3}=$1020.13,[/latex]

 

and if the interest is compounded daily [latex](365[/latex] times per year), we have [latex]$1020.20.[/latex] If we extend this concept, so that the interest is compounded continuously, after [latex]t[/latex] years we have

[latex]1000\underset{n\to \infty }{\text{lim}}{(1+\frac{0.02}{n})}^{nt}.[/latex]

 

Now let’s manipulate this expression so that we have an exponential growth function. Recall that the number [latex]e[/latex] can be expressed as a limit:

[latex]e=\underset{m\to \infty }{\text{lim}}{(1+\frac{1}{m})}^{m}.[/latex]

 

Based on this, we want the expression inside the parentheses to have the form [latex](1+1\text{/}m).[/latex] Let [latex]n=0.02m.[/latex] Note that as [latex]n\to \infty ,[/latex] [latex]m\to \infty [/latex] as well. Then we get

[latex]1000\underset{n\to \infty }{\text{lim}}{(1+\frac{0.02}{n})}^{nt}=1000\underset{m\to \infty }{\text{lim}}{(1+\frac{0.02}{0.02m})}^{0.02mt}=1000{\left[\underset{m\to \infty }{\text{lim}}{(1+\frac{1}{m})}^{m}\right]}^{0.02t}.[/latex]

 

We recognize the limit inside the brackets as the number [latex]e.[/latex] So, the balance in our bank account after [latex]t[/latex] years is given by [latex]1000{e}^{0.02t}.[/latex] Generalizing this concept, we see that if a bank account with an initial balance of [latex]$P[/latex] earns interest at a rate of [latex]r\text{%},[/latex] compounded continuously, then the balance of the account after [latex]t[/latex] years is

[latex]\text{Balance}=P{e}^{rt}.[/latex]

 

Example: Compound Interest

A 25-year-old student is offered an opportunity to invest some money in a retirement account that pays 5% annual interest compounded continuously. How much does the student need to invest today to have [latex]$1[/latex] million when she retires at age [latex]65?[/latex] What if she could earn 6% annual interest compounded continuously instead?

Try It

Suppose instead of investing at age [latex]25\sqrt{{b}^{2}-4ac},[/latex] the student waits until age 35. How much would she have to invest at [latex]5\text{%}?[/latex] At [latex]6\text{%}?[/latex]

Try It

If a quantity grows exponentially, the time it takes for the quantity to double remains constant. In other words, it takes the same amount of time for a population of bacteria to grow from 100 to 200 bacteria as it does to grow from 10,000 to 20,000 bacteria. This time is called the doubling time. To calculate the doubling time, we want to know when the quantity reaches twice its original size. So we have

[latex]\begin{array}{ccc}\hfill 2{y}_{0}& =\hfill & {y}_{0}{e}^{kt}\hfill \\ \hfill 2& =\hfill & {e}^{kt}\hfill \\ \hfill \text{ln}2& =\hfill & kt\hfill \\ \hfill t& =\hfill & \frac{\text{ln}2}{k}.\hfill \end{array}[/latex]

 

Definition

If a quantity grows exponentially, the doubling time is the amount of time it takes the quantity to double. It is given by

[latex]\text{Doubling time}=\frac{\text{ln}2}{k}.[/latex]

Example: Using the Doubling Time

Assume a population of fish grows exponentially. A pond is stocked initially with 500 fish. After 6 months, there are 1000 fish in the pond. The owner will allow his friends and neighbors to fish on his pond after the fish population reaches 10,000. When will the owner’s friends be allowed to fish?

Try It

Suppose it takes 9 months for the fish population in the last example to reach 1000 fish. Under these circumstances, how long do the owner’s friends have to wait?

Watch the following video to see the worked solution to the above Try It.

For closed captioning, open the video on its original page by clicking the Youtube logo in the lower right-hand corner of the video display. In YouTube, the video will begin at the same starting point as this clip, but will continue playing until the very end.

You can view the transcript for this segmented clip of “6.8 Try It Problems” here (opens in new window).

Try It