Learning Outcomes
- Evaluate algebraic expressions
- Evaluate trigonometric functions using the unit circle
- Use substitution to rewrite a mathematical equation
- Write the equation of a line using slope and a point on the line
In the Parametric Equations and Calculus of Parametric Equations sections, we will be working with parametric equations, graphing them, and using calculus to differentiate and integrate them. Here we will review how to evaluate both algebraic and trigonometric expressions, how to use substitution to rewrite a mathematical equation, and how to write the equation of a line.
Evaluate Algebraic Expressions
An algebraic expression is a collection of constants and variables joined together by the algebraic operations of addition, subtraction, multiplication, and division.
Example: Evaluating Algebraic Expressions
Evaluate each expression for the given values.
- [latex]x+5[/latex] for [latex]x=-5[/latex]
- [latex]\frac{t}{2t - 1}[/latex] for [latex]t=10[/latex]
- [latex]\dfrac{4}{3}\pi {r}^{3}[/latex] for [latex]r=5[/latex]
- [latex]a+ab+b[/latex] for [latex]a=11,b=-8[/latex]
- [latex]\sqrt{2{m}^{3}{n}^{2}}[/latex] for [latex]m=2,n=3[/latex]
Try It
Evaluate Trigonometric Functions Using the Unit Circle
It is easiest to evaluate trigonometric functions when an angle is in the first quadrant. When the original angle is given in quadrant two, three, or four, a reference angle should be found.
An angle’s reference angle is the acute angle, [latex]t[/latex], formed by the terminal side of the angle [latex]t[/latex] and the horizontal axis. A reference angle is always an angle between [latex]0[/latex] and [latex]90^\circ[/latex], or [latex]0[/latex] and [latex]\frac{\pi }{2}[/latex] radians. As we can see in the figure below, for any angle in quadrants II, III, or IV, there is a reference angle in quadrant I.

A visual of the corresponding reference angles for each of the quadrants.
How To: Given an angle between [latex]0[/latex] and [latex]2\pi[/latex], find its reference angle.
- An angle in the first quadrant is its own reference angle.
- For an angle in the second or third quadrant, the reference angle is [latex]|\pi -t|[/latex] or [latex]|180^\circ \mathrm{-t}|[/latex].
- For an angle in the fourth quadrant, the reference angle is [latex]2\pi -t[/latex] or [latex]360^\circ \mathrm{-t}[/latex].
- If an angle is less than [latex]0[/latex] or greater than [latex]2\pi[/latex], add or subtract [latex]2\pi[/latex] as many times as needed to find an equivalent angle between [latex]0[/latex] and [latex]2\pi[/latex].
Example: Finding a Reference Angle
Find the reference angle of [latex]225^\circ[/latex] as shown in below.
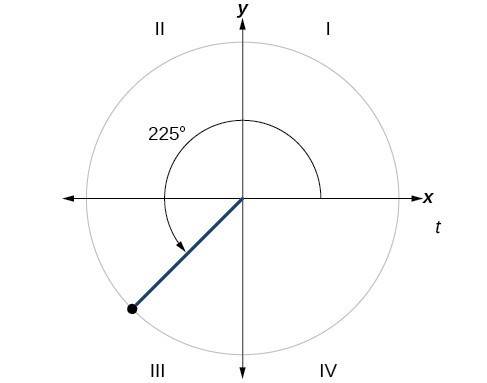
Try It
Find the reference angle of [latex]\frac{5\pi }{3}[/latex].
We can evaluate trigonometric functions of angles outside the first quadrant using reference angles. The quadrant of the original angle determines whether the answer is positive or negative. To help us remember which of the six trigonometric functions are positive in each quadrant, we can use the mnemonic phrase “A Smart Trig Class.” Each of the four words in the phrase corresponds to one of the four quadrants, starting with quadrant I and rotating counterclockwise. In quadrant I, which is “A,” all of the six trigonometric functions are positive. In quadrant II, “Smart,” only sine and its reciprocal function, cosecant, are positive. In quadrant III, “Trig,” only tangent and its reciprocal function, cotangent, are positive. Finally, in quadrant IV, “Class,” only cosine and its reciprocal function, secant, are positive.
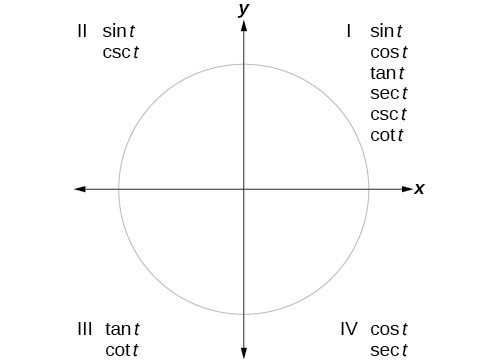
An illustration of which trigonometric functions are positive in each of the quadrants.
The unit circle tells us the value of cosine and sine at any of the given angle measures seen below. The first coordinate in each ordered pair is the value of cosine at the given angle measure, while the second coordinate in each ordered pair is the value of sine at the given angle measure. You will learn in Section 1.3 that all trigonometric functions can be written in terms of sine and cosine. Thus, if you can evaluate sine and cosine at various angle values, you can also evaluate the other trigonometric functions at various angle values. Take time to learn the [latex]\left(x,y\right)[/latex] coordinates of all of the major angles in the first quadrant of the unit circle.
Remember, every angle in quadrant two, three, or four has a reference angle that lies in quadrant one. The quadrant of the original angle only affects the sign (positive or negative) of a trigonometric function’s value at a given angle.
How To: Given the angle of a point on The Unit circle, find the Value of Cosine (Or Sine) using quadrant one.
- Find the reference angle using the appropriate reference angle formula from the first portion of this review section.
- Find the value of cosine (or sine) at the reference angle by looking at quadrant one of the unit circle.
- Determine the appropriate sign of your found value for cosine (or sine) based on the quadrant of the original angle.
Example: Using the Unit Circle to Find the Value of cosine
Use quadrant one of the unit circle to find the value of cosine at an angle of [latex]\frac{7\pi }{6}[/latex].
Try It
Use quadrant one of the unit circle to find the value of sine at an angle of [latex]\frac{5\pi }{3}[/latex].
Use Substitution to Rewrite a Mathematical Equation
Substitution can be used to rewrite a mathematical expression in terms of another variable.
Example: Using Substitution to Rewrite a Mathematical Expression
Rewrite the equation [latex]x=4t+3[/latex] in terms of [latex]y[/latex] using [latex]y=2t-1[/latex].
Try It
Rewrite the equation [latex]y=2t^{2}-1[/latex] in terms of [latex]x[/latex] using [latex]x=5-t[/latex].
Write the Equation of a Line
To write the equation of a line, the line’s slope and a point the line goes through must be known. Perhaps the most familiar form of a linear equation is slope-intercept form written as [latex]y=mx+b[/latex], where [latex]m=\text{slope}[/latex] and [latex]b=y\text{-intercept}[/latex]. Let us begin with the slope.
Often, the starting point to writing the equation of a line is to use point-slope formula. Given the slope and one point on a line, we can find the equation of the line using point-slope form shown below.
We need only one point and the slope of the line to use the formula. After substituting the slope and the coordinates of one point into the formula, we simplify it and write it in slope-intercept form.
A General Note: The Point-Slope Formula
Given one point and the slope, using point-slope form will lead to the equation of a line:
Example: Finding the Equation of a Line Given the Slope and One Point
Write the equation of the line with slope [latex]m=-3[/latex] and passing through the point [latex]\left(4,8\right)[/latex]. Write the final equation in slope-intercept form.
Try It
Given [latex]m=4[/latex], find the equation of the line in slope-intercept form passing through the point [latex]\left(2,5\right)[/latex].
Try It
Candela Citations
- Modification and Revision. Provided by: Lumen Learning. License: CC BY: Attribution
- College Algebra Corequisite. Provided by: Lumen Learning. Located at: https://courses.lumenlearning.com/waymakercollegealgebracorequisite/. License: CC BY: Attribution
- Precalculus. Provided by: Lumen Learning. Located at: https://courses.lumenlearning.com/precalculus/. License: CC BY: Attribution

