Learning Outcomes
- Identify reference angles for angles measured in both radians and degrees
- Evaluate trigonometric functions using the unit circle
- Evaluate inverse trigonometric functions
- Draw an Angle in Standard Position
- Write the equation of a circle in standard form
In the Polar Coordinates section, we will be introduced to polar coordinates and equations. Here we will review how to evaluate sine and cosine functions at specific angle measures, evaluate inverse trigonometric functions, draw angles, and write the equation of a circle in standard form.
Find Reference Angles
It is easiest to evaluate trigonometric functions when an angle is in the first quadrant. When the original angle is given in quadrant two, three, or four, a reference angle should be found.
An angle’s reference angle is the acute angle, [latex]t[/latex], formed by the terminal side of the angle [latex]t[/latex] and the horizontal axis. A reference angle is always an angle between [latex]0[/latex] and [latex]90^\circ [/latex], or [latex]0[/latex] and [latex]\frac{\pi }{2}[/latex] radians. As we can see in the figure below, for any angle in quadrants II, III, or IV, there is a reference angle in quadrant I.

A visual of the corresponding reference angles for each of the quadrants.
How To: Given an angle between [latex]0[/latex] and [latex]2\pi [/latex], find its reference angle
- An angle in the first quadrant is its own reference angle.
- For an angle in the second or third quadrant, the reference angle is [latex]|\pi -t|[/latex] or [latex]|180^\circ \mathrm{-t}|[/latex].
- For an angle in the fourth quadrant, the reference angle is [latex]2\pi -t[/latex] or [latex]360^\circ \mathrm{-t}[/latex].
- If an angle is less than [latex]0[/latex] or greater than [latex]2\pi [/latex], add or subtract [latex]2\pi [/latex] as many times as needed to find an equivalent angle between [latex]0[/latex] and [latex]2\pi [/latex].
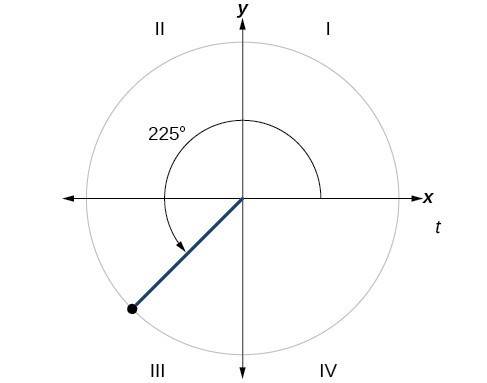
Example: Finding a Reference Angle
Find the reference angle of [latex]225^\circ [/latex] as shown in below.
Try It
Find the reference angle of [latex]\frac{5\pi }{3}[/latex].
We can evaluate trigonometric functions of angles outside the first quadrant using reference angles. The quadrant of the original angle determines whether the answer is positive or negative. To help us remember which of the six trigonometric functions are positive in each quadrant, we can use the mnemonic phrase “A Smart Trig Class.” Each of the four words in the phrase corresponds to one of the four quadrants, starting with quadrant I and rotating counterclockwise. In quadrant I, which is “A,” all of the six trigonometric functions are positive. In quadrant II, “Smart,” only sine and its reciprocal function, cosecant, are positive. In quadrant III, “Trig,” only tangent and its reciprocal function, cotangent, are positive. Finally, in quadrant IV, “Class,” only cosine and its reciprocal function, secant, are positive.
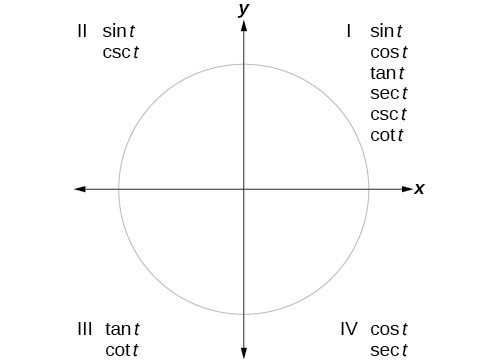
An illustration of which trigonometric functions are positive in each of the quadrants.
Evaluate Trigonometric Functions Using the Unit Circle
The unit circle tells us the value of cosine and sine at any of the given angle measures seen below. The first coordinate in each ordered pair is the value of cosine at the given angle measure, while the second coordinate in each ordered pair is the value of sine at the given angle measure. You will learn in Section 1.3 that all trigonometric functions can be written in terms of sine and cosine. Thus, if you can evaluate sine and cosine at various angle values, you can also evaluate the other trigonometric functions at various angle values. Take time to learn the [latex]\left(x,y\right)[/latex] coordinates of all of the major angles in the first quadrant of the unit circle.
Remember, every angle in quadrant two, three, or four has a reference angle that lies in quadrant one. The quadrant of the original angle only affects the sign (positive or negative) of a trigonometric function’s value at a given angle.
How To: Given the angle of a point on The Unit circle, find the Value of Cosine (Or Sine) using quadrant one.
- Find the reference angle using the appropriate reference angle formula from the first portion of this review section.
- Find the value of cosine (or sine) at the reference angle by looking at quadrant one of the unit circle.
- Determine the appropriate sign of your found value for cosine (or sine) based on the quadrant of the original angle.
Example: Using the Unit Circle to Find the Value of cosine
Use quadrant one of the unit circle to find the value of cosine at an angle of [latex]\frac{7\pi }{6}[/latex].
Try It
Use quadrant one of the unit circle to find the value of sine at an angle of [latex]\frac{5\pi }{3}[/latex].
Evaluate Inverse Trigonometric Functions
(also in Module 1, Skills Review for Integrals Resulting in Inverse Trigonometric Functions)
In order to use inverse trigonometric functions, we need to understand that an inverse trigonometric function “undoes” what the original trigonometric function “does,” as is the case with any other function and its inverse. In other words, the domain of the inverse function is the range of the original function, and vice versa, as summarized below.

For example, if [latex]f(x)=\sin x[/latex], then we would write [latex]f^{-1}(x)={\sin}^{-1}{x}[/latex]. Be aware that [latex]{\sin}^{-1}x[/latex] does not mean [latex]\frac{1}{\sin{x}}[/latex]. The following examples illustrate the inverse trigonometric functions:
- Since [latex]\sin\left(\frac{\pi}{6}\right)=\frac{1}{2}[/latex], then [latex]\frac{\pi}{6}=\sin^{−1}(\frac{1}{2})[/latex].
- Since [latex]\cos(\pi)=−1[/latex], then [latex]\pi=\cos^{−1}(−1)[/latex].
- Since [latex]\tan\left(\frac{\pi}{4}\right)=1[/latex], then [latex]\frac{\pi}{4}=\tan^{−1}(1)[/latex].
A General Note: Relations for Inverse Sine, Cosine, and Tangent Functions
For angles in the interval [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex], if [latex]\sin y=x[/latex], then [latex]\sin^{−1}x=y[/latex].
For angles in the interval [0, π], if [latex]\cos y=x[/latex], then [latex]\cos^{−1}x=y[/latex].
For angles in the interval [latex]\left(−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right)[/latex], if [latex]\tan y=x[/latex], then [latex]\tan^{−1}x=y[/latex].
Just as we did with the original trigonometric functions, we can give exact values for the inverse functions when we are using the special angles, specifically [latex]\frac{\pi}{ 6} (30^\circ)\text{, }\frac{\pi}{ 4} (45^\circ),\text{ and } \frac{\pi}{ 3} (60^\circ)[/latex], and their reflections into other quadrants.
How To: Given a “special” input value, evaluate an inverse trigonometric function.
- Find angle x for which the original trigonometric function has an output equal to the given input for the inverse trigonometric function.
- If x is not in the defined range of the inverse, find another angle y that is in the defined range and has the same sine, cosine, or tangent as x, depending on which corresponds to the given inverse function.
Example: Evaluating Inverse Trigonometric Functions for Special Input Values
Evaluate each of the following.
a. [latex]\sin−1\left(\frac{1}{2}\right)[/latex]
b. [latex]\sin−1\left(−\frac{2}{\sqrt{2}}\right)[/latex]
c. [latex]\cos−1\left(−\frac{3}{\sqrt{2}}\right)[/latex]
d. [latex]\tan^{− 1}(1)[/latex]
Try It
Evaluate each of the following.
- [latex]\sin^{−1}(−1)[/latex]
- [latex]\tan^{−1}(−1)[/latex]
- [latex]\cos^{−1}(−1)[/latex]
- [latex]\cos^{−1}(\frac{1}{2})[/latex]
Try It
Draw an Angle in Standard Position
Angle creation is a dynamic process. We start with two rays lying on top of one another. We leave one fixed in place, and rotate the other. The fixed ray is the initial side, and the rotated ray is the terminal side. The measure of an angle is the amount of rotation from the initial side to the terminal side. Probably the most familiar unit of angle measurement is the degree. One degree is [latex]\frac{1}{360}[/latex] of a circular rotation, so a complete circular rotation contains 360 degrees. An angle measured in degrees should always include the unit “degrees” after the number, or include the degree symbol °. For example, 90 degrees = 90°.
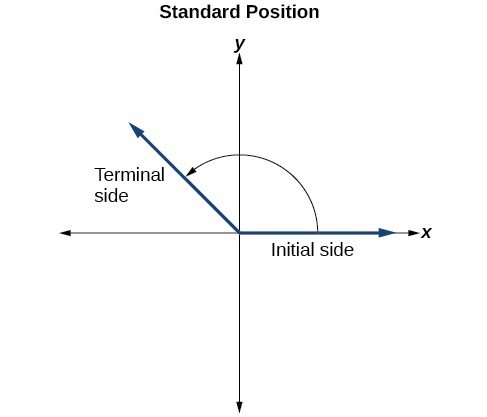
An angle has both an initial side and a terminal side.
When drawing an angle on an x–y coordinate plane, an angle is in standard position if its vertex is located at the origin, and its initial side extends along the positive x-axis.
If the angle is measured in a counterclockwise direction from the initial side to the terminal side, the angle is said to be a positive angle. If the angle is measured in a clockwise direction, the angle is said to be a negative angle.
HOW TO: GIVEN AN ANGLE MEASURE IN DEGREES, DRAW THE ANGLE IN STANDARD POSITION
- Express the angle measure as a fraction of 360°.
- Reduce the fraction to simplest form.
- Draw an angle that contains that same fraction of the circle, beginning on the positive x-axis and moving counterclockwise for positive angles and clockwise for negative angles.
Example: Drawing an Angle
- Sketch an angle of 30° in standard position.
- Sketch an angle of −135° in standard position.
TRY IT
Show an angle of 240° on a circle in standard position.
Write the Equation of a Circle in Standard Form
A circle is all points in a plane that are a fixed distance from a given point in the plane. The given point is called the center, (h,k), and the fixed distance is called the radius, r, of the circle.
Given a circle with center (h,k) and radius r, the equation of the circle in standard form is:
[latex](x-h)^2+(y-k)^2=r^2[/latex]
Example: Writing the Equation of a Circle in Standard Form
Write the equation of a circle in standard form with a center of (5,7) and a radius of 4.
Try It
Write the equation of a circle in standard form with a center of (4,-2) and a radius of 3.




