Skills Review for Partial Fractions

Learning Outcomes

Divide polynomials by binomials using synthetic division or long division
Factor the greatest common factor (monomial) of a polynomial
Factor a trinomial with a leading coefficient of 1
Rewrite a trinomial as a four term polynomial and factor by grouping terms
Factor difference of squares
Factor sum or difference of cubes
Solve rational equations by clearing denominators
Solve systems of equations

In the Partial Fractions section, we will learn how to split fractions that have multiple terms in the denominator. This will then allow us to evaluate the resulting “split” integral. Here we will review polynomial long division, factoring polynomials, simplifying rational equations, and solving systems of equations.

Perform Polynomial Long Division

We are familiar with the long division algorithm for ordinary arithmetic. We begin by dividing into the digits of the dividend that have the greatest place value. We divide, multiply, subtract, include the digit in the next place value position, and repeat. For example, let’s divide 178 by 3 using long division.
Long Division. Step 1, 5 times 3 equals 15 and 17 minus 15 equals 2. Step 2: Bring down the 8. Step 3: 9 times 3 equals 27 and 28 minus 27 equals 1. Answer: 59 with a remainder of 1 or 59 and one-third.

Another way to look at the solution is as a sum of parts. This should look familiar, since it is the same method used to check division in elementary arithmetic.

$\begin{array}{l}\left(\text{divisor }\cdot \text{ quotient}\right)\text{ + remainder}\text{ = dividend}\hfill \\ \left(3\cdot 59\right)+1 = 177+1 = 178\hfill \end{array}$

We call this the Division Algorithm and will discuss it more formally after looking at an example.

Division of polynomials that contain more than one term has similarities to long division of whole numbers. We can write a polynomial dividend as the product of the divisor and the quotient added to the remainder. The terms of the polynomial division correspond to the digits (and place values) of the whole number division. This method allows us to divide two polynomials. For example, if we were to divide $2{x}^{3}-3{x}^{2}+4x+5$ by $x+2$ using the long division algorithm, it would look like this:
Set up the division problem. 2x cubed divided by x is 2x squared. Multiply the sum of x and 2 by 2x squared. Subtract. Then bring down the next term. Negative 7x squared divided by x is negative 7x. Multiply the sum of x and 2 by negative 7x. Subtract, then bring down the next term. 18x divided by x is 18. Multiply the sum of x and 2 by 18. Subtract.

We have found

$\frac{2{x}^{3}-3{x}^{2}+4x+5}{x+2}=2{x}^{2}-7x+18-\frac{31}{x+2}$

$2{x}^{3}-3{x}^{2}+4x+5=\left(x+2\right)\left(2{x}^{2}-7x+18\right)-31$

We can identify the dividend, divisor, quotient, and remainder.

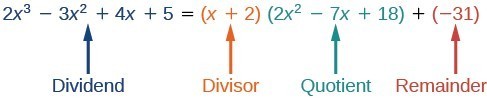
The dividend is 2x cubed minus 3x squared plus 4x plus 5. The divisor is x plus 2. The quotient is 2x squared minus 7x plus 18. The remainder is negative 31.

Writing the result in this manner illustrates the Division Algorithm.

How To: Given a polynomial and a binomial, use long division to divide the polynomial by the binomial

Set up the division problem.
Determine the first term of the quotient by dividing the leading term of the dividend by the leading term of the divisor.
Multiply the answer by the divisor and write it below the like terms of the dividend.
Subtract the bottom binomial from the terms above it.
Bring down the next term of the dividend.
Repeat steps 2–5 until reaching the last term of the dividend.
If the remainder is non-zero, express as a fraction using the divisor as the denominator.

Example: Using Long Division to Divide a Second-Degree Polynomial

Divide $5{x}^{2}+3x - 2$ by $x+1$ .

Show Solution

Set up the division problem. 5x squared divided by x is 5x. Multiply x plus 1 by 5x. Subtract. Bring down the next term. Negative 2x divded by x is negative 2. Multiply x + 1 by negative 2. Subtract. The quotient is $5x - 2$ . The remainder is 0. We write the result as

$\frac{5{x}^{2}+3x - 2}{x+1}=5x - 2$

$5{x}^{2}+3x - 2=\left(x+1\right)\left(5x - 2\right)$

Analysis of the Solution

This division problem had a remainder of 0. This tells us that the dividend is divided evenly by the divisor and that the divisor is a factor of the dividend.

Example: Using Long Division to Divide a Third-Degree Polynomial

Divide $6{x}^{3}+11{x}^{2}-31x+15$ by $3x - 2$ .

Show Solution

There is a remainder of 1. We can express the result as:

$\frac{6{x}^{3}+11{x}^{2}-31x+15}{3x - 2}=2{x}^{2}+5x - 7+\frac{1}{3x - 2}$

Analysis of the Solution

We can check our work by using the Division Algorithm to rewrite the solution then multiplying.

$\left(3x - 2\right)\left(2{x}^{2}+5x - 7\right)+1=6{x}^{3}+11{x}^{2}-31x+15$

Notice, as we write our result,

the dividend is $6{x}^{3}+11{x}^{2}-31x+15$
the divisor is $3x - 2$
the quotient is $2{x}^{2}+5x - 7$
the remainder is 1

Try It

Factor Polynomials

Recall that the greatest common factor (GCF) of two numbers is the largest number that divides evenly into both numbers. For example, $4$ is the GCF of $16$ and $20$ because it is the largest number that divides evenly into both $16$ and $20$ . The GCF of polynomials works the same way: $4x$ is the GCF of $16x$ and $20{x}^{2}$ because it is the largest polynomial that divides evenly into both $16x$ and $20{x}^{2}$ .

Finding and factoring out a GCF from a polynomial is the first skill involved in factoring polynomials.

Factor a GCF out of a Polynomial

When factoring a polynomial expression, our first step is to check to see if each term contains a common factor. If so, we factor out the greatest amount we can from each term. To make it less challenging to find this GCF of the polynomial terms, first look for the GCF of the coefficients, and then look for the GCF of the variables.

A General Note: Greatest Common Factor

The greatest common factor (GCF) of a polynomial is the largest polynomial that divides evenly into each term of the polynomial.

To factor out a GCF from a polynomial, first identify the greatest common factor of the terms. You can then use the distributive property “backwards” to rewrite the polynomial in a factored form. Recall that the distributive property of multiplication over addition states that a product of a number and a sum is the same as the sum of the products.

Distributive Property Forward and Backward

Forward: We distribute $a$ over $b+c$ .

$a\left(b+c\right)=ab+ac$ .

Backward: We factor $a$ out of $ab+ac$ .

$ab+ac=a\left(b+c\right)$ .

We have seen that we can distribute a factor over a sum or difference. Now we see that we can “undo” the distributive property with factoring.

Example: Factoring The Greatest Common Factor

Factor $25b^{3}+10b^{2}$ .

Show Solution

Find the GCF.

$\begin{array}{l}\,\,25b^{3}=5\cdot5\cdot{b}\cdot{b}\cdot{b}\\\,\,10b^{2}=5\cdot2\cdot{b}\cdot{b}\\\text{GCF}=5\cdot{b}\cdot{b}=5b^{2}\end{array}$

Rewrite each term with the GCF as one factor.

$\begin{array}{l}25b^{3} = 5b^{2}\cdot5b\\10b^{2}=5b^{2}\cdot2\end{array}$

Rewrite the polynomial using the factored terms in place of the original terms.

$5b^{2}\left(5b\right)+5b^{2}\left(2\right)$

Factor out the $5b^{2}$ .

$5b^{2}\left(5b+2\right)$

Answer

$5b^{2}\left(5b+2\right)$

Analysis

The factored form of the polynomial $25b^{3}+10b^{2}$ is $5b^{2}\left(5b+2\right)$ . You can check this by doing the multiplication. $5b^{2}\left(5b+2\right)=25b^{3}+10b^{2}$ .

Note that if you do not factor the greatest common factor at first, you can continue factoring, rather than start all over.

For example:

$\begin{array}{l}25b^{3}+10b^{2}=5\left(5b^{3}+2b^{2}\right)\,\,\,\,\,\,\,\,\,\,\,\text{Factor out }5.\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=5b^{2}\left(5b+2\right) \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{Factor out }b^{2}.\end{array}$

Notice that you arrive at the same simplified form whether you factor out the GCF immediately or if you pull out factors individually.

How To: Given a polynomial expression, factor out the greatest common factor

Identify the GCF of the coefficients.
Identify the GCF of the variables.
Combine to find the GCF of the expression.
Determine what the GCF needs to be multiplied by to obtain each term in the expression.
Write the factored expression as the product of the GCF and the sum of the terms we need to multiply by.

Example: Factoring the Greatest Common Factor

Factor $6{x}^{3}{y}^{3}+45{x}^{2}{y}^{2}+21xy$ .

Show Solution

First find the GCF of the expression. The GCF of $6,45$ , and $21$ is $3$ . The GCF of ${x}^{3},{x}^{2}$ , and $x$ is $x$ . (Note that the GCF of a set of expressions of the form ${x}^{n}$ will always be the lowest exponent.) The GCF of ${y}^{3},{y}^{2}$ , and $y$ is $y$ . Combine these to find the GCF of the polynomial, $3xy$ .

Next, determine what the GCF needs to be multiplied by to obtain each term of the polynomial. We find that $3xy\left(2{x}^{2}{y}^{2}\right)=6{x}^{3}{y}^{3}, 3xy\left(15xy\right)=45{x}^{2}{y}^{2}$ , and $3xy\left(7\right)=21xy$ .

Finally, write the factored expression as the product of the GCF and the sum of the terms we needed to multiply by.

(3 x y) (2 x^{2} y^{2} + 15 x y + 7)

$\left(3xy\right)\left(2{x}^{2}{y}^{2}+15xy+7\right)$

Analysis of the Solution

After factoring, we can check our work by multiplying. Use the distributive property to confirm that $\left(3xy\right)\left(2{x}^{2}{y}^{2}+15xy+7\right)=6{x}^{3}{y}^{3}+45{x}^{2}{y}^{2}+21xy$ .

Watch this video to see more examples of how to factor the GCF from a trinomial.

You can view the transcript for “Ex 2: Identify GCF and Factor a Trinomial” here (opens in new window).

Factor a Trinomial with Leading Coefficient 1

Although we should always begin by looking for a GCF, pulling out the GCF is not the only way that polynomial expressions can be factored. The polynomial ${x}^{2}+5x+6$ has a GCF of 1, but it can be written as the product of the factors $\left(x+2\right)$ and $\left(x+3\right)$ .

Trinomials of the form ${x}^{2}+bx+c$ can be factored by finding two numbers with a product of $c$ and a sum of $b$ . The trinomial ${x}^{2}+10x+16$ , for example, can be factored using the numbers $2$ and $8$ because the product of these numbers is $16$ and their sum is $10$ . The trinomial can be rewritten as the product of $\left(x+2\right)$ and $\left(x+8\right)$ .

A General Note: Factoring a Trinomial with Leading Coefficient 1

A trinomial of the form ${x}^{2}+bx+c$ can be written in factored form as $\left(x+p\right)\left(x+q\right)$ where $pq=c$ and $p+q=b$ .

Q & A

Can every trinomial be factored as a product of binomials?

No. Some polynomials cannot be factored. These polynomials are said to be prime.

How To: Given a trinomial in the form ${x}^{2}+bx+c$ , factor it

List factors of $c$ .
Find $p$ and $q$ , a pair of factors of $c$ with a sum of $b$ .
Write the factored expression $\left(x+p\right)\left(x+q\right)$ .

Example: Factoring a Trinomial with Leading Coefficient 1

Factor ${x}^{2}+2x - 15$ .

Show Solution

We have a trinomial with leading coefficient $1,b=2$ , and $c=-15$ . We need to find two numbers with a product of $-15$ and a sum of $2$ . In the table, we list factors until we find a pair with the desired sum.

Factors of $-15$	Sum of Factors
$1,-15$	$-14$
$-1,15$	$14$
$3,-5$	$-2$
$-3,5$	$2$

Now that we have identified $p$ and $q$ as $-3$ and $5$ , write the factored form as $\left(x - 3\right)\left(x+5\right)$ .

Analysis of the Solution

We can check our work by multiplying. Use FOIL to confirm that $\left(x - 3\right)\left(x+5\right)={x}^{2}+2x - 15$ .

Q & A

Does the order of the factors matter?

No. Multiplication is commutative, so the order of the factors does not matter.

Try It

Factor by Grouping

Trinomials with leading coefficients other than 1 are slightly more complicated to factor. For these trinomials, we can factor by grouping by dividing the x term into the sum of two terms, factoring each portion of the expression separately, and then factoring out the GCF of the entire expression. The trinomial $2{x}^{2}+5x+3$ can be rewritten as $\left(2x+3\right)\left(x+1\right)$ using this process. We begin by rewriting the original expression as $2{x}^{2}+2x+3x+3$ and then factor each portion of the expression to obtain $2x\left(x+1\right)+3\left(x+1\right)$ . We then pull out the GCF of $\left(x+1\right)$ to find the factored expression.

A General Note: Factor by Grouping

To factor a trinomial of the form $a{x}^{2}+bx+c$ by grouping, we find two numbers with a product of $ac$ and a sum of $b$ . We use these numbers to divide the $x$ term into the sum of two terms and factor each portion of the expression separately then factor out the GCF of the entire expression.

How To: Given a trinomial in the form $a{x}^{2}+bx+c$ , factor by grouping

List factors of $ac$ .
Find $p$ and $q$ , a pair of factors of $ac$ with a sum of $b$ .
Rewrite the original expression as $a{x}^{2}+px+qx+c$ .
Pull out the GCF of $a{x}^{2}+px$ .
Pull out the GCF of $qx+c$ .
Factor out the GCF of the expression.

Example: Factoring a Trinomial by Grouping

Factor $5{x}^{2}+7x - 6$ by grouping.

Show Solution

We have a trinomial with $a=5,b=7$ , and $c=-6$ . First, determine $ac=-30$ . We need to find two numbers with a product of $-30$ and a sum of $7$ . In the table, we list factors until we find a pair with the desired sum.

Factors of $-30$	Sum of Factors
$1,-30$	$-29$
$-1,30$	$29$
$2,-15$	$-13$
$-2,15$	$13$
$3,-10$	$-7$
$-3,10$	$7$

So $p=-3$ and $q=10$ .

\begin{array}{cc} 5 x^{2} - 3 x + 10 x - 6 & Rewrite the original expression as a x^{2} + p x + q x + c . \\ x (5 x - 3) + 2 (5 x - 3) & Factor out the GCF of each part . \\ (5 x - 3) (x + 2) & Factor out the GCF of the expression . \end{array}

$\begin{array}{cc}5{x}^{2}-3x+10x - 6 \hfill & \text{Rewrite the original expression as }a{x}^{2}+px+qx+c.\hfill \\ x\left(5x - 3\right)+2\left(5x - 3\right)\hfill & \text{Factor out the GCF of each part}.\hfill \\ \left(5x - 3\right)\left(x+2\right)\hfill & \text{Factor out the GCF}\text{ }\text{ of the expression}.\hfill \end{array}$

Analysis of the Solution

We can check our work by multiplying. Use FOIL to confirm that $\left(5x - 3\right)\left(x+2\right)=5{x}^{2}+7x - 6$ .

Try It

In the next video, we see another example of how to factor a trinomial by grouping.

You can view the transcript for “Factor a Trinomial in the Form ax^2+bx+c Using the Grouping Technique” here (opens in new window).

Factor a Difference of Squares

A difference of squares is a perfect square subtracted from a perfect square. Recall that a difference of squares can be rewritten as factors containing the same terms but opposite signs because the middle terms cancel each other out when the two factors are multiplied.

a^{2} - b^{2} = (a + b) (a - b)

${a}^{2}-{b}^{2}=\left(a+b\right)\left(a-b\right)$

$\\$

We can use this equation to factor any differences of squares.

A General Note: Differences of Squares

A difference of squares can be rewritten as two factors containing the same terms but opposite signs.

a^{2} - b^{2} = (a + b) (a - b)

${a}^{2}-{b}^{2}=\left(a+b\right)\left(a-b\right)$

How To: Given a difference of squares, factor it into binomials

Confirm that the first and last term are perfect squares.
Write the factored form as $\left(a+b\right)\left(a-b\right)$ .

Example: Factoring a Difference of Squares

Factor $9{x}^{2}-25$ .

Show Solution

Notice that $9{x}^{2}$ and $25$ are perfect squares because $9{x}^{2}={\left(3x\right)}^{2}$ and $25={5}^{2}$ . The polynomial represents a difference of squares and can be rewritten as $\left(3x+5\right)\left(3x - 5\right)$ .

Try It

Q & A

Is there a formula to factor the sum of squares?

No. A sum of squares cannot be factored.

Watch this video to see another example of how to factor a difference of squares.

You can view the transcript for “Ex: Factor a Difference of Squares” here (opens in new window).

Factor the Sum and Difference of Cubes

Now we will look at two new special products: the sum and difference of cubes. Although the sum of squares cannot be factored, the sum of cubes can be factored into a binomial and a trinomial.

a^{3} + b^{3} = (a + b) (a^{2} - a b + b^{2})

${a}^{3}+{b}^{3}=\left(a+b\right)\left({a}^{2}-ab+{b}^{2}\right)$

$\\$

Similarly, the sum of cubes can be factored into a binomial and a trinomial but with different signs.

a^{3} - b^{3} = (a - b) (a^{2} + a b + b^{2})

${a}^{3}-{b}^{3}=\left(a-b\right)\left({a}^{2}+ab+{b}^{2}\right)$

$\\$

We can use the acronym SOAP to remember the signs when factoring the sum or difference of cubes. The first letter of each word relates to the signs: Same Opposite Always Positive. For example, consider the following example.

x^{3} - 2^{3} = (x - 2) (x^{2} + 2 x + 4)

${x}^{3}-{2}^{3}=\left(x - 2\right)\left({x}^{2}+2x+4\right)$

The sign of the first 2 is the same as the sign between ${x}^{3}-{2}^{3}$ . The sign of the $2x$ term is opposite the sign between ${x}^{3}-{2}^{3}$ . And the sign of the last term, 4, is always positive.

A General Note: Sum and Difference of Cubes

We can factor the sum of two cubes as

a^{3} + b^{3} = (a + b) (a^{2} - a b + b^{2})

${a}^{3}+{b}^{3}=\left(a+b\right)\left({a}^{2}-ab+{b}^{2}\right)$

We can factor the difference of two cubes as

a^{3} - b^{3} = (a - b) (a^{2} + a b + b^{2})

${a}^{3}-{b}^{3}=\left(a-b\right)\left({a}^{2}+ab+{b}^{2}\right)$

How To: Given a sum of cubes or difference of cubes, factor it

Confirm that the first and last term are cubes, ${a}^{3}+{b}^{3}$ or ${a}^{3}-{b}^{3}$ .
For a sum of cubes, write the factored form as $\left(a+b\right)\left({a}^{2}-ab+{b}^{2}\right)$ . For a difference of cubes, write the factored form as $\left(a-b\right)\left({a}^{2}+ab+{b}^{2}\right)$ .

Example: Factoring a Sum of Cubes

Factor ${x}^{3}+512$ .

Show Solution

Notice that ${x}^{3}$ and $512$ are cubes because ${8}^{3}=512$ . Rewrite the sum of cubes as $\left(x+8\right)\left({x}^{2}-8x+64\right)$ .

Analysis of the Solution

After writing the sum of cubes this way, we might think we should check to see if the trinomial portion can be factored further. However, the trinomial portion cannot be factored, so we do not need to check.

Try It

Factor the sum of cubes $216{a}^{3}+{b}^{3}$ .

Show Solution

$\left(6a+b\right)\left(36{a}^{2}-6ab+{b}^{2}\right)$

Example: Factoring a Difference of Cubes

Factor $8{x}^{3}-125$ .

Show Solution

Notice that $8{x}^{3}$ and $125$ are cubes because $8{x}^{3}={\left(2x\right)}^{3}$ and $125={5}^{3}$ . Write the difference of cubes as $\left(2x - 5\right)\left(4{x}^{2}+10x+25\right)$ .

Analysis of the Solution

Just as with the sum of cubes, we will not be able to further factor the trinomial portion.

Try It

Factor the difference of cubes: $1,000{x}^{3}-1$ .

Show Solution

$\left(10x - 1\right)\left(100{x}^{2}+10x+1\right)$

Try It

In the following two video examples, we show more binomials that can be factored as a sum or difference of cubes.

You can view the transcript for “Ex 1: Factor a Sum or Difference of Cubes” here (opens in new window).

You can view the transcript for “Ex 3: Factor a Sum or Difference of Cubes” here (opens in new window).

Solve Rational Equations

Equations that contain rational expressions are called rational equations. For example, $\frac{2x+1}{4}=\frac{x}{3}$ is a rational equation. One of the most straightforward ways to solve a rational equation is to eliminate denominators with the common denominator and then use properties of equality to isolate the variable. This method is often used to solve linear equations that involve fractions as in the following example:

Solve $\frac{1}{2}x-3=2-\frac{3}{4}x$ by clearing the fractions in the equation first.

Multiply both sides of the equation by $4$ , the common denominator of the fractional coefficients.

$\begin{array}{c}\frac{1}{2}x-3=2-\frac{3}{4}x\\ 4\left(\frac{1}{2}x-3\right)=4\left(2-\frac{3}{4}x\right)\\\text{}\\\,\,\,\,4\left(\frac{1}{2}x\right)-4\left(3\right)=4\left(2\right)+4\left(-\frac{3}{4}x\right)\\2x-12=8-3x\\\underline{+3x}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{+3x}\\5x-12=8\,\,\,\,\,\,\,\,\\\,\,\,\,\,\,\,\underline{+12}\,\,\,\,\underline{+12} \\5x=20\\x=4\end{array}$

We could have found a common denominator and worked with fractions, but that often leads to more mistakes. We can apply the same idea to solving rational equations. The difference between a linear equation and a rational equation is that rational equations can have polynomials in the numerator and denominator of the fractions. This means that clearing the denominator may sometimes mean multiplying the whole rational equation by a polynomial. In the next example, we will clear the denominators of a rational equation with a term that has a polynomial in the numerator.

Example: Simplifying and Solving a Rational Equation

Solve the equation $\frac{x+5}{8}=\frac{7}{4}$ .

Show Solution

Find the least common denominator of $4$ and $8$ . Remember, to find the LCD, identify the greatest number of times each factor appears in each factorization. Here, $2$ appears $3$ times, so $2\cdot2\cdot2$ , or $8$ , will be the LCD.

Multiply both sides of the equation by the common denominator, $8$ , to keep the equation balanced and to eliminate the denominators.

$\begin{array}{r}8\cdot \frac{x+5}{8}=\frac{7}{4}\cdot 8\,\,\,\,\,\,\,\\\\\frac{8(x+5)}{8}=\frac{7(8)}{4}\,\,\,\,\,\,\\\\\frac{8}{8}\cdot (x+5)=\frac{7(4\cdot 2)}{4}\\\\\frac{8}{8}\cdot (x+5)=7\cdot 2\cdot \frac{4}{4}\\\\1\cdot (x+5)=14\cdot 1\,\,\,\end{array}$

Simplify and solve for x.

$\begin{array}{r}x+5=14\\x=9\,\,\,\end{array}$

Check the solution by substituting $9$ for x in the original equation.

$\begin{array}{r}\frac{x+5}{8}=\frac{7}{4}\\\\\frac{9+5}{8}=\frac{7}{4}\\\\\frac{14}{8}=\frac{7}{4}\\\\\frac{7}{4}=\frac{7}{4}\end{array}$

Therefore, $x=9$ .

In the next example, we show how to solve a rational equation with a binomial in the denominator of one term. We will use the common denominator to eliminate the denominators from both fractions. Note that the LCD is the product of both denominators because they do not share any common factors.

Example: Simplifying and Solving a Rational Equation

Solve the equation $\frac{8}{x+1}=\frac{4}{3}$ .

Show Solution

Clear the denominators by multiplying each side by the common denominator. The common denominator is $3\left(x+1\right)$ since $3\text{ and }x+1$ do not have any common factors.

$\begin{array}{c}3\left(x+1\right)\left(\frac{8}{x+1}\right)=3\left(x+1\right)\left(\frac{4}{3}\right)\end{array}$

Simplify common factors.

$\begin{array}{c}3\cancel{\left(x+1\right)}\left(\frac{8}{\cancel{x+1}}\right)=\cancel{3}\left(x+1\right)\left(\frac{4}{\cancel{3}}\right)\\24=4\left(x+1\right)\\24=4x+4\end{array}$

Now this looks like a linear equation, and we can use the addition and multiplication properties of equality to solve it.

$\begin{array}{c}24=4x+4\\\underline{-4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-4}\\20=4x\,\,\,\,\,\,\,\,\\\\x=5\,\,\,\,\,\,\,\,\,\end{array}$

Check the solution in the original equation.

$\begin{array}{r}\,\,\,\,\,\frac{8}{\left(x+1\right)}=\frac{4}{3}\\\\\frac{8}{\left(5+1\right)}=\frac{4}{3}\\\\\frac{8}{6}=\frac{4}{3}\\\frac{4}{3}=\frac{4}{3}\end{array}$

Therefore, $x=5$ .

TRY IT

Solve the equation $\dfrac{3}{x-2}=\dfrac{1}{x-1}+\dfrac{7}{(x-1)(x-2)}$ .

Show Solution

x=4[\latex]

TRY IT

Solve Systems of Equations

A system of linear equations consists of two or more linear equations made up of two or more variables such that all equations in the system are considered simultaneously. To find the unique solution to a system of linear equations, we must find a numerical value for each variable in the system that will satisfy all equations in the system at the same time. Some linear systems may not have a solution and others may have an infinite number of solutions. In order for a linear system to have a unique solution, there must be at least as many equations as there are variables. Even so, this does not guarantee a unique solution.

We will first look at systems of linear equations in two variables, which consist of two equations that contain two different variables. For example, consider the following system of linear equations in two variables.

\begin{matrix} 2 x + y = 15 \\ 3 x - y = 5 \end{matrix}

$\begin{gathered}2x+y=15\\ 3x-y=5\end{gathered}$

The solution to a system of linear equations in two variables is any ordered pair that satisfies each equation independently. In this example, the ordered pair (4, 7) is the solution to the system of linear equations. We can verify the solution by substituting the values into each equation to see if the ordered pair satisfies both equations. Shortly we will investigate methods of finding such a solution if it exists.

\begin{aligned} 2 (4) + (7) & = 15 & True \\ 3 (4) - (7) & = 5 & True \end{aligned}

$\begin{align}2\left(4\right)+\left(7\right)&=15&&\text{True} \\ 3\left(4\right)-\left(7\right)&=5&&\text{True} \end{align}$

Two of the most common ways to solve a system of linear equations are the substitution method and the addition (elimination) method.

The Substitution Method

How To: Given a system of two equations in two variables, solve using the substitution method.

Solve one of the two equations for one of the variables in terms of the other.
Substitute the expression for this variable into the second equation, then solve for the remaining variable.
Substitute that solution into either of the original equations to find the value of the first variable. If possible, write the solution as an ordered pair.
Check the solution in both equations.

Example: Solving a System of Equations Using The Substitution Method

Solve the following system of equations by substitution.

$\begin{gathered}-x+y=-5 \\ 2x - 5y=1 \end{gathered}$

Show Solution

First, we will solve the first equation for $y$ .

$\begin{gathered}-x+y=-5 \\ y=x - 5 \end{gathered}$

Now we can substitute the expression $x - 5$ for $y$ in the second equation.

$\begin{gathered}2x - 5y=1\\ 2x - 5\left(x - 5\right)=1\\ 2x - 5x+25=1\\ -3x=-24\\ x=8\end{gathered}$

Now, we substitute $x=8$ into the first equation and solve for $y$ .

$\begin{gathered}-\left(8\right)+y=-5 \\ y=3 \end{gathered}$

Our solution is $\left(8,3\right)$ .

Check the solution by substituting $\left(8,3\right)$ into both equations.

$\begin{align}-x+y&=-5\\ -\left(8\right)+\left(3\right)&=-5&& \text{True} \\ 2x - 5y&=1 \\ 2\left(8\right)-5\left(3\right)&=1&& \text{True} \end{align}$

Try It

The Addition (Elimination) Method

How To: Given a system of equations, solve using the addition method.

Write both equations with x- and y-variables on the left side of the equal sign and constants on the right.
Write one equation above the other, lining up corresponding variables. If one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, add the equations together, eliminating one variable. If not, use multiplication by a nonzero number so that one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, then add the equations to eliminate the variable.
Solve the resulting equation for the remaining variable.
Substitute that value into one of the original equations and solve for the second variable.
Check the solution by substituting the values into the other equation.

Example: Solving a System of Equations Using The Addition Method

Solve the given system of equations by addition.

$\begin{gathered}x+2y=-1 \\ -x+y=3 \end{gathered}$

Show Solution

Both equations are already set equal to a constant. Notice that the coefficient of $x$ in the second equation, –1, is the opposite of the coefficient of $x$ in the first equation, 1. We can add the two equations to eliminate $x$ without needing to multiply by a constant.

$\begin{align} x+2y&=-1 \\ -x+y&=3 \\ \hline 3y&=2\end{align}$

Now that we have eliminated $x$ , we can solve the resulting equation for $y$ .

$\begin{gathered}3y=2 \\ y=\frac{2}{3} \end{gathered}$

Then, we substitute this value for $y$ into one of the original equations and solve for $x$ .

$\begin{gathered}-x+y=3 \\ -x+\frac{2}{3}=3\\ -x=3-\frac{2}{3}\\ -x=\frac{7}{3}\\ x=-\frac{7}{3} \end{gathered}$

The solution to this system is $\left(-\frac{7}{3},\frac{2}{3}\right)$ .

Check the solution in the first equation.

$\begin{align}x+2y&=\left(-\frac{7}{3}\right)+2\left(\frac{2}{3}\right) \\&=-\frac{7}{3}+\frac{4}{3} \\ &=-\frac{3}{3}=-1&& \text{True} \end{align}$

Example: Solving a System of Equations Using The Addition Method

Solve the given system of equations in two variables by addition.

$\begin{gathered}2x+3y=-16\\ 5x - 10y=30\end{gathered}$

Show Solution

One equation has $2x$ and the other has $5x$ . The least common multiple is $10x$ so we will have to multiply both equations by a constant in order to eliminate one variable. Let’s eliminate $x$ by multiplying the first equation by $-5$ and the second equation by $2$ .

$\begin{align} -5\left(2x+3y\right)&=-5\left(-16\right) \\ -10x - 15y&=80 \\ 2\left(5x - 10y\right)&=2\left(30\right) \\ 10x - 20y&=60 \end{align}$

Then, we add the two equations together.

$\begin{align}\ −10x−15y&=80 \\ 10x−20y&=60 \\ \hline −35y&=140 \\ y&=−4 \end{align}$

Substitute $y=-4$ into the original first equation.

$\begin{gathered}2x+3\left(-4\right)=-16\\ 2x - 12=-16\\ 2x=-4\\ x=-2\end{gathered}$

The solution is $\left(-2,-4\right)$ . Check it in the other equation.

$\begin{align}5x - 10y&= 5\left(-2\right)-10\left(-4\right) \\ &=-10+40 \\ &=30\end{align}$

Try It

Solve the system of equations by addition.

$\begin{gathered}2x - 7y=2\\ 3x+y=-20\end{gathered}$

Show Solution

$\left(-6,-2\right)$

Systems of Equations Containing Three Variables

How To: Given a linear system of three equations, solve for three unknowns.

Pick any pair of equations and solve for one variable.
Pick another pair of equations and solve for the same variable.
You have created a system of two equations in two unknowns. Solve the resulting two-by-two system.
Back-substitute known variables into any one of the original equations and solve for the missing variable.

Example: Solving a System of Equations Containing Three Variables

Find a solution to the following system:

$\begin{align}x - 2y+3z&=9&& \text{(1)} \\ -x+3y-z&=-6&& \text{(2)} \\ 2x - 5y+5z&=17&& \text{(3)} \end{align}$

Show Solution

There will always be several choices as to where to begin, but the most obvious first step here is to eliminate $x$ by adding equations (1) and (2).

$\begin{align}x - 2y+3z&=9 \\ -x+3y-z&=-6 \\ \hline y+2z&=3 \end{align}$ $\begin{align} &&\text{(1)} \\ &&(2) \\ &&\text{(4)} \end{align}$

The second step is multiplying equation (1) by $-2$ and adding the result to equation (3). These two steps will eliminate the variable $x$ .

$\begin{align}−2x+4y−6z&=−18 \\ 2x−5y+5z&=17 \\ \hline−y−z=−1\end{align}$ $\begin{align} &&\left(1\right)&\text{ multiplied by }−2 \\ &&\left(3\right)& \\&&\left(5\right)&\end{align}$

In equations (4) and (5), we have created a new two-by-two system. We can solve for $z$ by adding the two equations.

$\begin{align}y+2z&=3 \\ -y-z&=-1 \\ \hline z&=2\end{align}$ $\begin{align}&&(4) \\ &&(5) \\ &&(6) \end{align}$

Choosing one equation from each new system, we obtain the upper triangular form:

$\begin{align}x - 2y+3z&=9&& \left(1\right) \\ y+2z&=3&& \left(4\right) \\ z&=2&& \left(6\right) \end{align}$

Next, we back-substitute $z=2$ into equation (4) and solve for $y$ .

$\begin{gathered}y+2\left(2\right)=3 \\ y+4=3 \\ y=-1 \end{gathered}$

Finally, we can back-substitute $z=2$ and $y=-1$ into equation (1). This will yield the solution for $x$

$\begin{gathered} x - 2\left(-1\right)+3\left(2\right)=9\\ x+2+6=9\\ x=1\end{gathered}$

The solution is the ordered triple $\left(1,-1,2\right)$ .

Try It

Solve the system of equations in three variables.

$\begin{align}2x+y - 2z&=-1 \\ 3x - 3y-z&=5 \\ x - 2y+3z&=6 \end{align}$

Show Solution

$\left(1,-1,1\right)$

Techniques of Integration: Prerequisite Material