Learning Outcomes
- Complete the square
- Evaluate trigonometric functions using right triangles
In the Trigonometric Substitution section, we will learn how to evaluate integrals that contain square roots with a strictly numeric quantity and variable quantity either added or subtracted. Each of these quantities can be rewritten as a quantity squared followed by applying a trigonometric substitution formula. Here we will review how to complete the square and evaluate trigonometric functions at an arbitrary angle [latex]\theta[/latex].
Complete the Square
Completing the square can be used to create a perfect square trinomial which factors into a binomial squared. To complete the square, we add or subtract terms to both sides of the equation until we have a perfect square trinomial on one side of the equal sign. Here is an example.
We will use the example [latex]{x}^{2}+4x+1[/latex] to illustrate each step. To complete the square, the leading coefficient, a, must equal 1. If it does not, then divide the entire equation by a. Then, we can use the following procedures to complete the square and factor the resulting perfect square trinomial.
- Multiply the b term by [latex]\frac{1}{2}[/latex] and square it.
[latex]\begin{array}{l}\frac{1}{2}\left(4\right)=2\hfill \\ {2}^{2}=4\hfill \end{array}[/latex]
- Add and subtract [latex]{\left(\frac{1}{2}b\right)}^{2}[/latex] to the expression. Simplify the original constant term and the subtracted perfect square trinomial constant. We have
[latex]\begin{array}{l}{x}^{2}+4x+4+1-4\hfill \\ = {x}^{2}+4x+4-3\hfill \end{array}[/latex]
- The first three terms can now be factored as a perfect square trinomial.
[latex]\begin{array}{l}{x}^{2}+4x+4-3\hfill \\ ={\left(x+2\right)}^{2}-3\hfill \end{array}[/latex]
Example: Create a perfect square trinomial using the method of complete the square
Complete the square on: [latex]3\left(x^2 - 10x\right)[/latex].
try it
Evaluate Trigonometric Functions Using Right Triangles
When working with right triangles, the same rules apply regardless of the orientation of the triangle. In fact, we can evaluate the six trigonometric functions of either of the two acute angles in the triangle below.
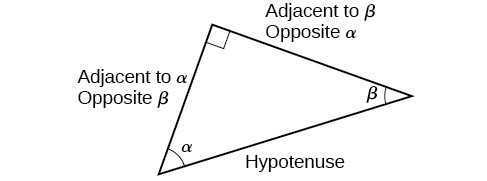
We will be asked to find all six trigonometric functions for a given angle in a triangle. Often, the strategy is to find the sine, cosine, and tangent of the angles first. Then, we can find the other trigonometric functions easily because we know that the reciprocal of sine is cosecant, the reciprocal of cosine is secant, and the reciprocal of tangent is cotangent.
How To: Given the side lengths of a right triangle, evaluate the six trigonometric functions of one of the acute angles.
- If needed, draw the right triangle and label the angle provided.
- Identify the angle, the adjacent side, the side opposite the angle, and the hypotenuse of the right triangle.
- Find the required function:
- sine as the ratio of the opposite side to the hypotenuse
- cosine as the ratio of the adjacent side to the hypotenuse
- tangent as the ratio of the opposite side to the adjacent side
- secant as the ratio of the hypotenuse to the adjacent side
- cosecant as the ratio of the hypotenuse to the opposite side
- cotangent as the ratio of the adjacent side to the opposite side
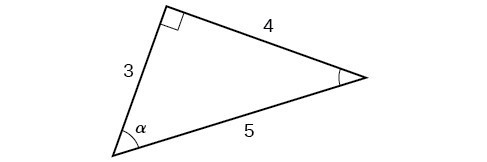
Example: Using a Right Triangle To EValuate All Six Trigonometric Functions
Using the triangle shown below, evaluate [latex]\sin \alpha[/latex], [latex]\cos \alpha[/latex], [latex]\tan \alpha[/latex], [latex]\sec \alpha[/latex], [latex]\csc \alpha [/latex], and [latex]\cot \alpha[/latex].
Try It
Using the triangle shown below, evaluate [latex]\sin t[/latex], [latex]\cos t[/latex], [latex]\tan t[/latex], [latex]\sec t[/latex], [latex]\csc t[/latex], and [latex]\cot t[/latex].
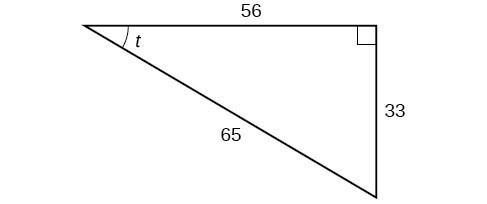
Try It
Hint: The Pythagorean Theorem can be used to find the length of the missing side.
