The Alternating Series Test

Learning Outcomes

Use the alternating series test to test an alternating series for convergence
Estimate the sum of an alternating series

A series whose terms alternate between positive and negative values is an alternating series. For example, the series

\sum_{n = 1}^{\infty} {(- \frac{1}{2})}^{n} = - \frac{1}{2} + \frac{1}{4} - \frac{1}{8} + \frac{1}{16} - \dots

$\displaystyle\sum _{n=1}^{\infty }{\left(-\frac{1}{2}\right)}^{n}=-\frac{1}{2}+\frac{1}{4}-\frac{1}{8}+\frac{1}{16}-\cdots$

and

\sum_{n = 1}^{\infty} \frac{{(- 1)}^{n + 1}}{n} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \dots

$\displaystyle\sum _{n=1}^{\infty }\frac{{\left(-1\right)}^{n+1}}{n}=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots$

are both alternating series.

Definition

Any series whose terms alternate between positive and negative values is called an alternating series. An alternating series can be written in the form

\sum_{n = 1}^{\infty} {(- 1)}^{n + 1} b_{n} = b_{1} - b_{2} + b_{3} - b_{4} + \dots

$\displaystyle\sum _{n=1}^{\infty }{\left(-1\right)}^{n+1}{b}_{n}={b}_{1}-{b}_{2}+{b}_{3}-{b}_{4}+\cdots$

\sum_{n - 1}^{\infty} {(- 1)}^{n} b_{n} = - b_{1} + b_{2} - b_{3} + b_{4} - \dots

$\displaystyle\sum _{n - 1}^{\infty }{\left(-1\right)}^{n}{b}_{n}=\text{-}{b}_{1}+{b}_{2}-{b}_{3}+{b}_{4}-\cdots$

Where ${b}_{n}\ge 0$ for all positive integers n.

Series (1), shown as the first alternating series example, is a geometric series. Since $|r|=|\text{-}\frac{1}{2}|<1$ , the series converges. Series (2), shown as the second alternating series example, is called the alternating harmonic series. We will show that whereas the harmonic series diverges, the alternating harmonic series converges.

To prove this, we look at the sequence of partial sums $\left\{{S}_{k}\right\}$ (Figure 1).

Proof

Consider the odd terms ${S}_{2k+1}$ for $k\ge 0$ . Since $\frac{1}{\left(2k+1\right)}<\frac{1}{2k}$ ,

S_{2 k + 1} = S_{2 k - 1} - \frac{1}{2 k} + \frac{1}{2 k + 1} < S_{2 k - 1}

${S}_{2k+1}={S}_{2k - 1}-\frac{1}{2k}+\frac{1}{2k+1}<{S}_{2k - 1}$ .

Therefore, $\left\{{S}_{2k+1}\right\}$ is a decreasing sequence. Also,

S_{2 k + 1} = (1 - \frac{1}{2}) + (\frac{1}{3} - \frac{1}{4}) + \dots + (\frac{1}{2 k - 1} - \frac{1}{2 k}) + \frac{1}{2 k + 1} > 0

${S}_{2k+1}=\left(1-\frac{1}{2}\right)+\left(\frac{1}{3}-\frac{1}{4}\right)+\cdots +\left(\frac{1}{2k - 1}-\frac{1}{2k}\right)+\frac{1}{2k+1}>0$ .

Therefore, $\left\{{S}_{2k+1}\right\}$ is bounded below. Since $\left\{{S}_{2k+1}\right\}$ is a decreasing sequence that is bounded below, by the Monotone Convergence Theorem, $\left\{{S}_{2k+1}\right\}$ converges. Similarly, the even terms $\left\{{S}_{2k}\right\}$ form an increasing sequence that is bounded above because

S_{2 k} = S_{2 k - 2} + \frac{1}{2 k - 1} - \frac{1}{2 k} > S_{2 k - 2}

${S}_{2k}={S}_{2k - 2}+\frac{1}{2k - 1}-\frac{1}{2k}>{S}_{2k - 2}$

and

S_{2 k} = 1 + (- \frac{1}{2} + \frac{1}{3}) + \dots + (- \frac{1}{2 k - 2} + \frac{1}{2 k - 1}) - \frac{1}{2 k} < 1

${S}_{2k}=1+\left(-\frac{1}{2}+\frac{1}{3}\right)+\cdots +\left(-\frac{1}{2k - 2}+\frac{1}{2k - 1}\right)-\frac{1}{2k}<1$ .

Therefore, by the Monotone Convergence Theorem, the sequence $\left\{{S}_{2k}\right\}$ also converges. Since

S_{2 k + 1} = S_{2 k} + \frac{1}{2 k + 1}

${S}_{2k+1}={S}_{2k}+\frac{1}{2k+1}$ ,

we know that

lim_{k \to \infty} S_{2 k + 1} = lim_{k \to \infty} S_{2 k} + lim_{k \to \infty} \frac{1}{2 k + 1}

$\underset{k\to \infty }{\text{lim}}{S}_{2k+1}=\underset{k\to \infty }{\text{lim}}{S}_{2k}+\underset{k\to \infty }{\text{lim}}\frac{1}{2k+1}$ .

Letting $S=\underset{k\to \infty }{\text{lim}}{S}_{2k+1}$ and using the fact that $\frac{1}{\left(2k+1\right)}\to 0$ , we conclude that $\underset{k\to \infty }{\text{lim}}{S}_{2k}=S$ . Since the odd terms and the even terms in the sequence of partial sums converge to the same limit $S$ , it can be shown that the sequence of partial sums converges to $S$ , and therefore the alternating harmonic series converges to $S$ .

It can also be shown that $S=\text{ln}2$ , and we can write

\sum_{n = 1}^{\infty} \frac{{(- 1)}^{n + 1}}{n} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \dots = ln (2)

$\displaystyle\sum _{n=1}^{\infty }\frac{{\left(-1\right)}^{n+1}}{n}=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots =\text{ln}\left(2\right)$ .

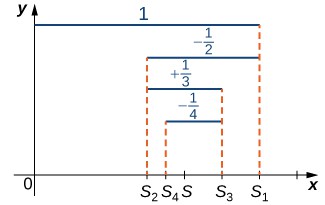
This graph demonstrates the alternating hamanic series in the first quadrant. The highest line 1 is drawn to S1, the next line -1/2 is drawn to S2, the next line +1/3 is drawn to S3, the line -1/4 is drawn to S4, and the last line +1/5 is drawn to S5. The odd terms are decreasing and bounded below, and the even terms are increasing and bounded above. It seems to be converging to S, which is in the middle of S2, S4 and S5, S3, S1.

$_\blacksquare$

More generally, any alternating series of form (3) or (4) (see the definition) converges as long as ${b}_{1}\ge {b}_{2}\ge {b}_{3}\ge \cdots$ and ${b}_{n}\to 0$ (Figure 2). The proof is similar to the proof for the alternating harmonic series.

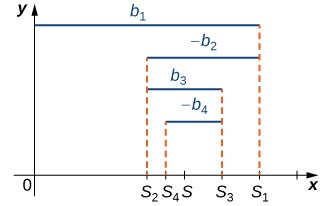
This diagram illustrates an alternating series in quadrant 1. The highest line b1 is drawn out to S1, the next line –b2 is drawn back to S2, the next line b3 is drawn out to S3, the next line –b4 is drawn back to S4, and the last line is drawn out to S5. It seems to be converging to S, which is in between S2, S4 and S5, S3, and S1. The odd terms are decreasing and bounded below. The even terms are increasing and bounded above.

theorem: Alternating Series Test

An alternating series of the form

\sum_{n = 1}^{\infty} {(- 1)}^{n + 1} b_{n} or \sum_{n = 1}^{\infty} {(- 1)}^{n} b_{n}

$\displaystyle\sum _{n=1}^{\infty }{\left(-1\right)}^{n+1}{b}_{n}\text{or}\displaystyle\sum _{n=1}^{\infty }{\left(-1\right)}^{n}{b}_{n}$

converges if

$0\le {b}_{n+1}\le {b}_{n}$ for all $n\ge 1$ and
$\underset{n\to \infty }{\text{lim}}{b}_{n}=0$ .

This is known as the alternating series test.

We remark that this theorem is true more generally as long as there exists some integer $N$ such that $0\le {b}_{n+1}\le {b}_{n}$ for all $n\ge N$ .

Example: Convergence of Alternating Series

For each of the following alternating series, determine whether the series converges or diverges.

$\displaystyle\sum _{n=1}^{\infty }\frac{{\left(-1\right)}^{n+1}}{{n}^{2}}$
$\displaystyle\sum _{n=1}^{\infty }\frac{{\left(-1\right)}^{n+1}n}{\left(n+1\right)}$

Show Solution

Since
$\frac{1}{{\left(n+1\right)}^{2}}<\frac{1}{{n}^{2}}\text{ and }\frac{1}{{n}^{2}}\to 0$ ,

the series converges.
Since $\frac{n}{\left(n+1\right)}\nrightarrow 0$ as $n\to \infty$ , we cannot apply the alternating series test. Instead, we use the nth term test for divergence. Since
$\underset{n\to \infty }{\text{lim}}\frac{{\left(-1\right)}^{n+1}n}{n+1}\ne 0$ ,

the series diverges.

try it

Determine whether the series $\displaystyle\sum _{n=1}^{\infty }\frac{{\left(-1\right)}^{n+1}n}{{2}^{n}}$ converges or diverges.

Hint

Is $\left\{\frac{n}{{2}^{n}}\right\}$ decreasing? What is $\underset{n\to \infty }{\text{lim}}\frac{n}{{2}^{n}}\text{?}$

Show Solution

Watch the following video to see the worked solution to the above Try IT.

For closed captioning, open the video on its original page by clicking the Youtube logo in the lower right-hand corner of the video display. In YouTube, the video will begin at the same starting point as this clip, but will continue playing until the very end.

You can view the transcript for this segmented clip of “5.5.1” here (opens in new window).

Try It

Remainder of an Alternating Series

It is difficult to explicitly calculate the sum of most alternating series, so typically the sum is approximated by using a partial sum. When doing so, we are interested in the amount of error in our approximation. Consider an alternating series

\sum_{n = 1}^{\infty} {(- 1)}^{n + 1} b_{n}

$\displaystyle\sum _{n=1}^{\infty }{\left(-1\right)}^{n+1}{b}_{n}$

satisfying the hypotheses of the alternating series test. Let $S$ denote the sum of this series and $\left\{{S}_{k}\right\}$ be the corresponding sequence of partial sums. From Figure 2, we see that for any integer $N\ge 1$ , the remainder ${R}_{N}$ satisfies

| R_{N} | = | S - S_{N} | \leq | S_{N + 1} - S_{N} | = b_{n + 1}

$|{R}_{N}|=|S-{S}_{N}|\le |{S}_{N+1}-{S}_{N}|={b}_{n+1}$ .

theorem: Remainders in Alternating Series

Consider an alternating series of the form

\sum_{n = 1}^{\infty} {(- 1)}^{n + 1} b_{n} or \sum_{n = 1}^{\infty} {(- 1)}^{n} b_{n}

$\displaystyle\sum _{n=1}^{\infty }{\left(-1\right)}^{n+1}{b}_{n}\text{or}\displaystyle\sum _{n=1}^{\infty }{\left(-1\right)}^{n}{b}_{n}$

that satisfies the hypotheses of the alternating series test. Let $S$ denote the sum of the series and ${S}_{N}$ denote the $N\text{th}$ partial sum. For any integer $N\ge 1$ , the remainder ${R}_{N}=S-{S}_{N}$ satisfies

| R_{N} | \leq b_{N + 1}

$|{R}_{N}|\le {b}_{N+1}$ .

In other words, if the conditions of the alternating series test apply, then the error in approximating the infinite series by the $N\text{th}$ partial sum ${S}_{N}$ is in magnitude at most the size of the next term ${b}_{N+1}$ .

Example: Estimating the Remainder of an Alternating Series

Consider the alternating series

\sum_{n = 1}^{\infty} \frac{{(- 1)}^{n + 1}}{n^{2}}

$\displaystyle\sum _{n=1}^{\infty }\frac{{\left(-1\right)}^{n+1}}{{n}^{2}}$ .

Use the remainder estimate to determine a bound on the error ${R}_{10}$ if we approximate the sum of the series by the partial sum ${S}_{10}$ .

Show Solution

From the theorem stated above,

$|{R}_{10}|\le {b}_{11}=\frac{1}{{11}^{2}}\approx 0.008265$ .

try it

Find a bound for ${R}_{20}$ when approximating $\displaystyle\sum _{n=1}^{\infty }\frac{{\left(-1\right)}^{n+1}}{n}$ by ${S}_{20}$ .

Hint

$|{R}_{20}|\le {b}_{21}$

Show Solution

$0.04762$

Module 5: Sequences and Series