Learning Outcomes
- Solve systems of equations
- Evaluate the determinant of a 2 x 2 matrix
In the Nonhomogeneous Linear Equations section, we will learn how to solve yet another type of second-order differential equation. Here we will review how to solve systems of equations in two variables and evaluate the determinant of a 2 x 2 matrix.
Solve a System of Equations in Two Variables
(also in Module 4, Skills Review for Maxima/Minima Problems and Lagrange Multipliers)
A system of linear equations consists of two or more linear equations made up of two or more variables such that all equations in the system are considered simultaneously. To find the unique solution to a system of linear equations, we must find a numerical value for each variable in the system that will satisfy all equations in the system at the same time. Some linear systems may not have a solution and others may have an infinite number of solutions. In order for a linear system to have a unique solution, there must be at least as many equations as there are variables. Even so, this does not guarantee a unique solution.
We will first look at systems of linear equations in two variables, which consist of two equations that contain two different variables. For example, consider the following system of linear equations in two variables.
The solution to a system of linear equations in two variables is any ordered pair that satisfies each equation independently. In this example, the ordered pair (4, 7) is the solution to the system of linear equations. We can verify the solution by substituting the values into each equation to see if the ordered pair satisfies both equations. Shortly we will investigate methods of finding such a solution if it exists.
Two of the most common ways to solve a system of linear equations are the substitution method and the addition (elimination) method.
The Substitution Method
How To: Given a system of two equations in two variables, solve using the substitution method.
- Solve one of the two equations for one of the variables in terms of the other.
- Substitute the expression for this variable into the second equation, then solve for the remaining variable.
- Substitute that solution into either of the original equations to find the value of the first variable. If possible, write the solution as an ordered pair.
- Check the solution in both equations.
EXAMPLE: SOLVING A SYSTEM OF EQUATIONS USING THE SUBSTITUTION METHOD
Solve the following system of equations by substitution.
[latex]\begin{align}-x+y&=-5 \\ 2x-5y&=1 \end{align}[/latex]
Try It
The Addition (Elimination) Method
How To: Given a system of equations, solve using the addition method.
- Write both equations with x– and y-variables on the left side of the equal sign and constants on the right.
- Write one equation above the other, lining up corresponding variables. If one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, add the equations together, eliminating one variable. If not, use multiplication by a nonzero number so that one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, then add the equations to eliminate the variable.
- Solve the resulting equation for the remaining variable.
- Substitute that value into one of the original equations and solve for the second variable.
- Check the solution by substituting the values into the other equation.
Example: SOLVING A SYSTEM OF EQUATIONS USING THE ADDITION METHOD
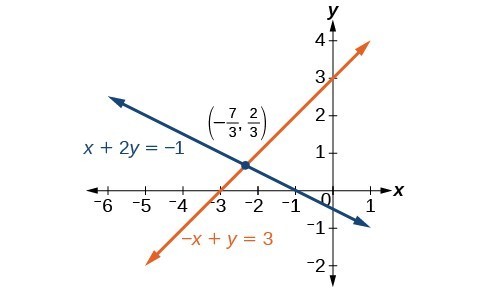
Solve the given system of equations by addition.
[latex]\begin{align}x+2y&=-1 \\ -x+y&=3 \end{align}[/latex]
Example: SOLVING A SYSTEM OF EQUATIONS USING THE ADDITION METHOD
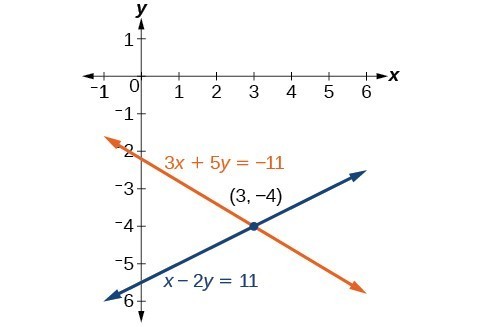
Solve the given system of equations by the addition method.
[latex]\begin{align}3x+5y&=-11 \\ x - 2y&=11 \end{align}[/latex]
Evaluate the Determinant of a 2×2 Matrix
(also in Module 2, Skills Review for the Dot Product, Cross Product, and Equations of Lines and Planes in Space)
A determinant is a real number that can be very useful in mathematics because it has multiple applications, such as calculating area, volume, and other quantities. Here, we will use determinants to reveal whether a matrix is invertible by using the entries of a square matrix to determine whether there is a solution to the system of equations. Perhaps one of the more interesting applications, however, is their use in cryptography. Secure signals or messages are sometimes sent encoded in a matrix. The data can only be decrypted with an invertible matrix and the determinant. For our purposes, we focus on the determinant as an indication of the invertibility of the matrix. Calculating the determinant of a matrix involves following the specific patterns that are outlined in this section.
A General Note: Find the Determinant of a 2 × 2 Matrix
The determinant of a [latex]2\text{ }\times \text{ }2[/latex] matrix, given
is defined as
Notice the change in notation. There are several ways to indicate the determinant, including [latex]\mathrm{det}\left(A\right)[/latex] and replacing the brackets in a matrix with straight lines, [latex]|A|[/latex].
Example: Finding the Determinant of a 2 × 2 Matrix
Find the determinant of the given matrix.
[latex]A=\left[\begin{array}{cc}5& 2\\ -6& 3\end{array}\right][/latex]
