Writing Equations in [latex]\mathbb{R}^3[/latex]

Now that we can represent points in space and find the distance between them, we can learn how to write equations of geometric objects such as lines, planes, and curved surfaces in [latex]\mathbb{R}^3[/latex]. First, we start with a simple equation. Compare the graphs of the equation [latex]x=0[/latex] in [latex]\mathbb{R}[/latex], [latex]\mathbb{R}^2[/latex], and [latex]\mathbb{R}^3[/latex] (Figure 1). From these graphs, we can see the same equation can describe a point, a line, or a plane.

Figure 1. (a) In [latex]ℝ[/latex], the equation [latex]x=0[/latex] describes a single point. (b) In [latex]ℝ^2[/latex], the equation [latex]x=0[/latex] describes a line, the [latex]y[/latex]-axis. (c) In [latex]ℝ^3[/latex], the equation [latex]x=0[/latex] describes a plane, the [latex]yz[/latex]-plane.

In space, the equation [latex]x=0[/latex] describes all points [latex](0, y, z)[/latex]. This equation defines the [latex]yz[/latex]-plane. Similarly, the [latex]xy[/latex]-plane contains all points of the form [latex](x, y, 0)[/latex]. The equation [latex]z=0[/latex] defines the [latex]xy[/latex]-plane and the equation [latex]y=0[/latex] describes the [latex]xz[/latex]-plane (Figure 2).

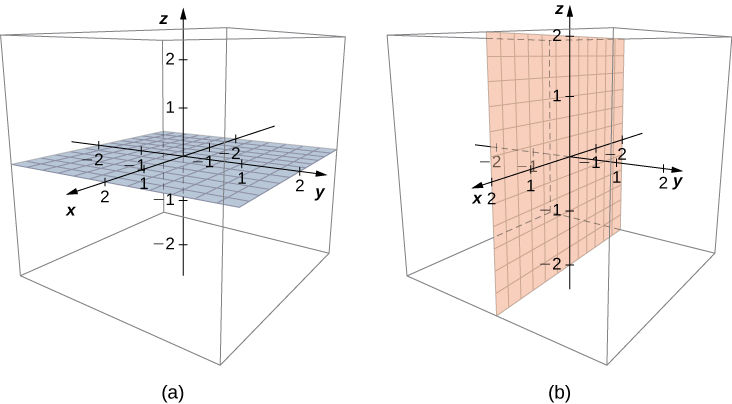
Figure 2 (a) In space, the equation [latex]z=0[/latex] describes the [latex]xy[/latex]-plane. (b) All points in the [latex]xz[/latex]-plane satisfy the equation [latex]y=0[/latex].

Understanding the equations of the coordinate planes allows us to write an equation for any plane that is parallel to one of the coordinate planes. When a plane is parallel to the [latex]xy[/latex]-plane, for example, the [latex]z[/latex]-coordinate of each point in the plane has the same constant value. Only the [latex]x[/latex]– and [latex]y[/latex]-coordinates of points in that plane vary from point to point.

definition

---

A sphere is the set of all points in space equidistant from a fixed point, the center of the sphere (Figure 3), just as the set of all points in a plane that are equidistant from the center represents a circle. In a sphere, as in a circle, the distance from the center to a point on the sphere is called the radius.

Figure 3. Each point [latex](x,y,z)[/latex] on the surface of a sphere is [latex]r[/latex] units away from the center [latex](a,b,c)[/latex].

The equation of a circle is derived using the distance formula in two dimensions. In the same way, the equation of a sphere is based on the three-dimensional formula for distance.

rule: equation of a sphere

---

The sphere with center [latex](a, b, c)[/latex] and radius [latex]r[/latex] can be represented by the equation

[latex](x - a)^2 +(y - b)^2+ (z - c)^2 =r^2[/latex]

.

This equation is known as the standard equation of a sphere.

Example: finding the equation of a sphere

Find the standard equation of the sphere with center [latex](10, 7, 4)[/latex] and point [latex](-1, 3, -2)[/latex] as shown in Figure 4.

Figure 4. The sphere centered at [latex](10,7,4)[/latex] containing point [latex](−1,3,−2)[/latex].

Show Solution

Use the distance formula to find the radius [latex]r[/latex] of the sphere:

[latex]\begin{align*} r &= \sqrt{(-1 - 10)^2 + (3-7)^2 + (-2 - 4)^2}\\ &= \sqrt{(-11)^2 + (-4)^2 + (-6)^2}\\ &= \sqrt{173} \end{align*}[/latex].

The standard equation of the sphere is

[latex](x-10)^2 + (y-7)^2+ (z-4)^2 = 173[/latex].

try it

Find the standard equation of the sphere with center [latex](-2, 4, 5)[/latex] containing point [latex](4, 4, -1)[/latex].

Show Solution

[latex](x+2)^2 + (y-4)^2+ (z+5)^2 = 52[/latex].

Example: finding the equation of a sphere

Let [latex]P=(-5, 2, 3)[/latex] and [latex]Q=(3, 4, -1)[/latex], and suppose line segment [latex]PQ[/latex] forms the diameter of a sphere (Figure 5). Find the equation of the sphere.

Figure 5. Line segment [latex]PQ[/latex].

Show Solution

Since [latex]PQ[/latex] is a diameter of the sphere, we know the center of the sphere is the midpoint of [latex]PQ[/latex]. Then,

[latex]\begin{align*} C &= (\frac{-5+3}{2}, \frac{2+4}{2}, \frac{3+(-1)}{2})\\ &= (-1, 3, 1)\\ \end{align*}[/latex].

Furthermore, we know the radius of the sphere is half the length of the diameter. This gives

[latex]\begin{align*} r &= \frac{1}{2}\sqrt{(-5 - 3)^2 + (2-4)^2 + (3 - (-1))^2}\\ &= \frac{1}{2}\sqrt{64+4+16}\\ &= \sqrt{21} \end{align*}[/latex].

.

Then, the equation of the sphere is [latex](x+1)^2 + (y-3)^2 + (z-1)^2 = 21[/latex].

try it

Find the equation of the sphere with diameter [latex]PQ[/latex], where [latex]P=(2, -1, -3)[/latex] and [latex]Q=(-2, 5, -1)[/latex].

Show Solution

[latex]x^2 + (y-2)^2 + (z+2)^2 = 14[/latex]

Watch the following video to see the worked solution to the above Try IT.

You can view the transcript for “CP 2.15” here (opens in new window)

Example: graphing other equations in three dimensions

Describe the set of points that satisfies [latex](x-4)(z-2)=0[/latex], and graph the set.

Show Solution

We must have either [latex]x-4=0[/latex] or [latex]z-2=0[/latex], so the set of points forms the two planes [latex]x=4[/latex] and [latex]z=2[/latex] (Figure 6).

Figure 6. The set of points satisfying [latex](x−4)(z−2)=0[/latex] forms the two planes [latex]x=4[/latex] and [latex]z=2[/latex].

try it

Describe the set of points that satisfies [latex](y+2)(z-3)=0[/latex], and graph the set.

Show Solution

The set of points forms the two planes [latex]y=-2[/latex] and [latex]z=3[/latex]. 

Figure 7. The set of points forms the two planes [latex]y=−2[/latex] and [latex]z=3[/latex].

Example: graphing other equations in three dimensions

Describe the set of points in three-dimensional space that satisfies [latex](x+2)^{2}+(y-1)^{2}=4[/latex], and graph the set.

Show Solution

The [latex]x[/latex]– and [latex]y[/latex]-coordinates form a circle in the [latex]xy[/latex]-plane of radius 2, centered at [latex](2, 1)[/latex]. Since there is no restriction on the [latex]z[/latex]-coordinate, the three-dimensional result is a circular cylinder of radius 2 centered on the line with [latex]x=2[/latex] and [latex]x=1[/latex]. The cylinder extends indefinitely in the [latex]z[/latex]-direction (Figure 8).

Figure 8. The set of points satisfying [latex](x−2)^2+(y−1)^2=4[/latex]. This is a cylinder of radius [latex]2[/latex] centered on the line with [latex]x=2[/latex] and [latex]y=1[/latex].

try it

Describe the set of points in three dimensional space that satisfies [latex]x^{2}+(z-2)^{2}=16[/latex], and graph the surface.

Show Solution

A cylinder of radius 4 centered on the line with [latex]x=0[/latex] and [latex]z=2[/latex]. 

Figure 9. A cylinder of radius [latex]4[/latex] centered on the line with [latex]x=0[/latex] and [latex]z=2[/latex].

Watch the following video to see the worked solution to the above Try IT.

You can view the transcript for “CP 2.17” here (opens in new window)