Polar Covalent Bonds: Electronegativity
Objectives
After completing this section, you should be able to
- describe how differences in electronegativity give rise to bond polarity.
- arrange a given series of the elements most often encountered in organic chemistry (C, H, O, S, P and the halogens) in order of increasing or decreasing electronegativity, without referring to a table of electronegativities.
- predict the positive and negative ends of a given bond formed between any two of the elements listed in Objective 2, above, without the use of a table of electronegativities or a periodic table.
- predict the positive and negative ends of a given bond formed between any two elements not listed in Objective 2, above, using a periodic table.
Key Terms
Make certain that you can define, and use in context, the key terms below.
- electronegativity inductive effect
- polar colvalent bond
Study Notes
Students often wonder why it is important to be able to tell whether a given bond is polar or not, and why they need to know which atoms carry a partial positive charge and which a partial negative charge. Consider the chloromethane (CH3Cl) molecule. The carbon atom is shown as carrying a partial positive charge. Now, recall that opposite charges attract. Thus, it seems reasonable that the slightly positive carbon atom in chloromethane should be susceptible to attack by a negatively charged species, such as the hydroxide ion, OH−. This theory is borne out in practice: hydroxide ions react with chloromethane by attacking the slightly positive carbon atom in the latter. It is often possible to rationalize chemical reactions in this manner, and you will find the knowledge of bond polarity indispensible when you start to write reaction mechanisms. Note: Because of the small difference in electronegativity between carbon and hydrogen, the C-H bond is normally assumed to be nonpolar.
Electronegativity
The elements with the highest ionization energies are generally those with the most negative electron affinities, which are located toward the upper right corner of the periodic table. Conversely, the elements with the lowest ionization energies are generally those with the least negative electron affinities and are located in the lower left corner of the periodic table.
Because the tendency of an element to gain or lose electrons is so important in determining its chemistry, various methods have been developed to quantitatively describe this tendency. The most important method uses a measurement called electronegativity (represented by the Greek letter chi, χ, pronounced “ky” as in “sky”), defined as the relative ability of an atom to attract electrons to itself in a chemical compound. Elements with high electronegativities tend to acquire electrons in chemical reactions and are found in the upper right corner of the periodic table. Elements with low electronegativities tend to lose electrons in chemical reactions and are found in the lower left corner of the periodic table.
Unlike ionization energy or electron affinity, the electronegativity of an atom is not a simple, fixed property that can be directly measured in a single experiment. In fact, an atom’s electronegativity should depend to some extent on its chemical environment because the properties of an atom are influenced by its neighbors in a chemical compound. Nevertheless, when different methods for measuring the electronegativity of an atom are compared, they all tend to assign similar relative values to a given element. For example, all scales predict that fluorine has the highest electronegativity and cesium the lowest of the stable elements, which suggests that all the methods are measuring the same fundamental property.
Note
Electronegativity is defined as the ability of an atom in a particular molecule to attract electrons to itself. The greater the value, the greater the attractiveness for electrons.
Unfortunately there is no direct way of measuring electronegativity. Dipole-moment measurements tell us about the electrical behavior of all electron pairs in the molecule, not just the bonding pair in which we are interested. Also, the polarity of a bond depends on whether the bond is a single, double, or triple bond and on what the other atoms and electron pairs in a molecule are. Therefore the dipole moment cannot tell us quantitatively the difference between the electronegativities of two bonded atoms. Various attempts have been made over the years to derive a scale of electronegativities for the elements, none of which is entirely satisfactory. Nevertheless most of these attempts agree in large measure in telling us which elements are more electronegative than others. The best-known of these scales was devised by the Nobel prize-winning California chemist Linus Pauling (1901 to 1994) and is shown in the periodic table found below. In this scale a value of 4.0 is arbitrarily given to the most electronegative element, fluorine, and the other electronegativities are scaled relative to this value.
Electronegativities of the elements
| → Atomic radius decreases → Ionization energy increases → Electronegativity increases → | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Group (vertical) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
| Period (horizontal) | |||||||||||||||||||
| 1 | H 2.20 |
He | |||||||||||||||||
| 2 | Li 0.98 |
Be 1.57 |
B 2.04 |
C 2.55 |
N 3.04 |
O 3.44 |
F 3.98 |
Ne | |||||||||||
| 3 | Na 0.93 |
Mg 1.31 |
Al 1.61 |
Si 1.90 |
P 2.19 |
S 2.58 |
Cl 3.16 |
Ar | |||||||||||
| 4 | K 0.82 |
Ca 1.00 |
Sc 1.36 |
Ti 1.54 |
V 1.63 |
Cr 1.66 |
Mn 1.55 |
Fe 1.83 |
Co 1.88 |
Ni 1.91 |
Cu 1.90 |
Zn 1.65 |
Ga 1.81 |
Ge 2.01 |
As 2.18 |
Se 2.55 |
Br 2.96 |
Kr 3.00 |
|
| 5 | Rb 0.82 |
Sr 0.95 |
Y 1.22 |
Zr 1.33 |
Nb 1.6 |
Mo 2.16 |
Tc 1.9 |
Ru 2.2 |
Rh 2.28 |
Pd 2.20 |
Ag 1.93 |
Cd 1.69 |
In 1.78 |
Sn 1.96 |
Sb 2.05 |
Te 2.1 |
I 2.66 |
Xe 2.60 |
|
| 6 | Cs 0.79 |
Ba 0.89 |
* | Hf 1.3 |
Ta 1.5 |
W 2.36 |
Re 1.9 |
Os 2.2 |
Ir 2.20 |
Pt 2.28 |
Au 2.54 |
Hg 2.00 |
Tl 1.62 |
Pb 2.33 |
Bi 2.02 |
Po 2.0 |
At 2.2 |
Rn 2.2 |
|
| 7 | Fr 0.7 |
Ra 0.9 |
** | Rf | Db | Sg | Bh | Hs | Mt | Ds | Rg | Cn | Uut | Uuq | Uup | Uuh | Uus | Uuo | |
| Lanthanoids | * | La 1.1 |
Ce 1.12 |
Pr 1.13 |
Nd 1.14 |
Pm 1.13 |
Sm 1.17 |
Eu 1.2 |
Gd 1.2 |
Tb 1.1 |
Dy 1.22 |
Ho 1.23 |
Er 1.24 |
Tm 1.25 |
Yb 1.1 |
Lu 1.27 |
|||
| Actinoids | ** | Ac 1.1 |
Th 1.3 |
Pa 1.5 |
U 1.38 |
Np 1.36 |
Pu 1.28 |
Am 1.13 |
Cm 1.28 |
Bk 1.3 |
Cf 1.3 |
Es 1.3 |
Fm 1.3 |
Md 1.3 |
No 1.3 |
Lr 1.3 |
|||
What if two atoms of equal electronegativity bond together?
Consider a bond between two atoms, A and B. If the atoms are equally electronegative, both have the same tendency to attract the bonding pair of electrons, and so it will be found on average half way between the two atoms:
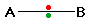
To get a bond like this, A and B would usually have to be the same atom. You will find this sort of bond in, for example, H2 or Cl2 molecules. Note: It’s important to realize that this is an average picture. The electrons are actually in a molecular orbital, and are moving around all the time within that orbital. This sort of bond could be thought of as being a “pure” covalent bond – where the electrons are shared evenly between the two atoms.
What if B is slightly more electronegative than A?
B will attract the electron pair rather more than A does.
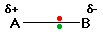
That means that the B end of the bond has more than its fair share of electron density and so becomes slightly negative. At the same time, the A end (rather short of electrons) becomes slightly positive. In the diagram, “$$\delta$$” (read as “delta”) means “slightly” – so $$\delta+$$ means “slightly positive”.
A polar bond is a covalent bond in which there is a separation of charge between one end and the other – in other words in which one end is slightly positive and the other slightly negative. Examples include most covalent bonds. The hydrogen-chlorine bond in HCl or the hydrogen-oxygen bonds in water are typical.

If B is a lot more electronegative than A, then the electron pair is dragged right over to B’s end of the bond. To all intents and purposes, A has lost control of its electron, and B has complete control over both electrons. Ions have been formed. The bond is then an ionic bond rather than a covalent bond.
A “spectrum” of bonds
The implication of all this is that there is no clear-cut division between covalent and ionic bonds. In a pure covalent bond, the electrons are held on average exactly half way between the atoms. In a polar bond, the electrons have been dragged slightly towards one end. How far does this dragging have to go before the bond counts as ionic? There is no real answer to that. Sodium chloride is typiclly considered an ionic solid, but even here the sodium has not completely lost control of its electron. Because of the properties of sodium chloride, however, we tend to count it as if it were purely ionic. Lithium iodide, on the other hand, would be described as being “ionic with some covalent character”. In this case, the pair of electrons has not moved entirely over to the iodine end of the bond. Lithium iodide, for example, dissolves in organic solvents like ethanol – not something which ionic substances normally do.
Summary
- No electronegativity difference between two atoms leads to a pure non-polar covalent bond.
- A small electronegativity difference leads to a polar covalent bond.
- A large electronegativity difference leads to an ionic bond.
Example 1: Polar Bonds vs. Polar Molecules
In a simple diatomic molecule like HCl, if the bond is polar, then the whole molecule is polar. What about more complicated molecules?
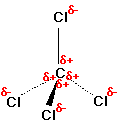
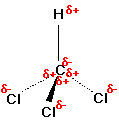
Figure: (left) CCl4 (right) CHCl3
Consider CCl4, (left panel in figure above), which as a molecule is not polar – in the sense that it doesn’t have an end (or a side) which is slightly negative and one which is slightly positive. The whole of the outside of the molecule is somewhat negative, but there is no overall separation of charge from top to bottom, or from left to right.
In contrast, CHCl3 is a polar molecule (right panel in figure above). The hydrogen at the top of the molecule is less electronegative than carbon and so is slightly positive. This means that the molecule now has a slightly positive “top” and a slightly negative “bottom”, and so is overall a polar molecule.
A polar molecule will need to be “lop-sided” in some way.
Molecular Dipole Moments
You previously learned how to calculate the dipole moments of simple diatomic molecules. In more complex molecules with polar covalent bonds, the three-dimensional geometry and the compound’s symmetry determine whether there is a net dipole moment. Mathematically, dipole moments are vectors; they possess both a magnitude and a direction. The dipole moment of a molecule is therefore the vector sum of the dipole moments of the individual bonds in the molecule. If the individual bond dipole moments cancel one another, there is no net dipole moment. Such is the case for CO2, a linear molecule (part (a) in Figure 2.1.1). Each C–O bond in CO2 is polar, yet experiments show that the CO2 molecule has no dipole moment. Because the two C–O bond dipoles in CO2 are equal in magnitude and oriented at 180° to each other, they cancel. As a result, the CO2 molecule has no net dipole moment even though it has a substantial separation of charge. In contrast, the H2O molecule is not linear (part (b) in Figure 2.1.1); it is bent in three-dimensional space, so the dipole moments do not cancel each other. Thus a molecule such as H2O has a net dipole moment. We expect the concentration of negative charge to be on the oxygen, the more electronegative atom, and positive charge on the two hydrogens. This charge polarization allows H2O to hydrogen-bond to other polarized or charged species, including other water molecules.
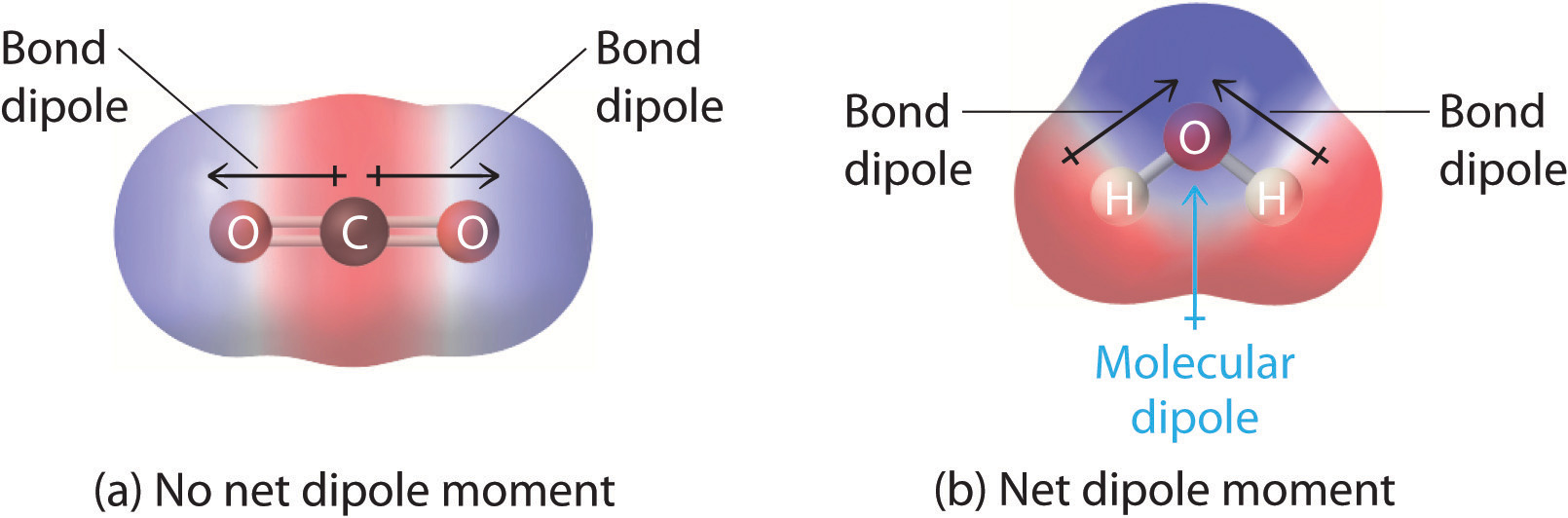
Figure: How Individual Bond Dipole Moments Are Added Together to Give an Overall Molecular Dipole Moment for Two Triatomic Molecules with Different Structures. (a) In CO2, the C–O bond dipoles are equal in magnitude but oriented in opposite directions (at 180°). Their vector sum is zero, so CO2 therefore has no net dipole. (b) In H2O, the O–H bond dipoles are also equal in magnitude, but they are oriented at 104.5° to each other. Hence the vector sum is not zero, and H2O has a net dipole moment.
Other examples of molecules with polar bonds are shown in Figure 2.1.2. In molecular geometries that are highly symmetrical (most notably tetrahedral and square planar, trigonal bipyramidal, and octahedral), individual bond dipole moments completely cancel, and there is no net dipole moment. Although a molecule like CHCl3 is best described as tetrahedral, the atoms bonded to carbon are not identical. Consequently, the bond dipole moments cannot cancel one another, and the molecule has a dipole moment. Due to the arrangement of the bonds in molecules that have V-shaped, trigonal pyramidal, seesaw, T-shaped, and square pyramidal geometries, the bond dipole moments cannot cancel one another. Consequently, molecules with these geometries always have a nonzero dipole moment.

Figure: Molecules with Polar Bonds. Individual bond dipole moments are indicated in red. Due to their different three-dimensional structures, some molecules with polar bonds have a net dipole moment (HCl, CH2O, NH3, and CHCl3), indicated in blue, whereas others do not because the bond dipole moments cancel (BCl3, CCl4, PF5, and SF6).
Note
Molecules with asymmetrical charge distributions have a net dipole moment.
Example
Which molecule(s) has a net dipole moment?
- H2S
- NHF2
- BF3
Given: three chemical compounds
Asked for: net dipole moment
Strategy:
For each three-dimensional molecular geometry, predict whether the bond dipoles cancel. If they do not, then the molecule has a net dipole moment.
Example
Which molecule(s) has a net dipole moment?
- CH3Cl
- SO3
- XeO3
Example
Rank the following from least polar to most polar using knowledge of electronegativity
CH3CH2-Li CH3CH2-K CH3CH2-F CH3CH2-OH
Contributors
- Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
- Prof. Steven Farmer (Sonoma State University)
- Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)
- Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.
- Jim Clark (Chemguide.co.uk)


