Learning Objectives
Determine slope of a line using the slope formula.
Perform fraction arithmetic.
Determine the linear function given:
- a slope and the [latex]y[/latex]-intercept
- a slope and a point
- two points
- a graph
- a point and a parallel linear function
- a point and a perpendicular linear function
Slope
The slope of a line, [latex]m[/latex], is a measure of the steepness of the line, and since the steepness is the same all along the line, the slope is constant. The slope of a line is defined as the ratio of [latex]\frac{\text{rise}}{\text{run}}[/latex] where rise is the change in [latex]y[/latex]-values, [latex]\Delta y[/latex], and run is the corresponding change in [latex]x[/latex]-values, [latex]\Delta x[/latex]. If [latex]y=f(x)[/latex], then slope = [latex]\frac{\Delta y}{\Delta x}=\frac{\text{change in function values}}{\text{change in }x\text{-values}}[/latex].
Consider the line in figure 1. It passes through the points (–4, –4) and (10, 3). The run is the distance between [latex]x=-4[/latex] and [latex]x=10[/latex]; a total of 14 units. Rather than counting units on the graph, we can subtract the two [latex]x[/latex]-coordinates: 10 – (–4) = 14. The rise is the distance between [latex]y=-4[/latex] and [latex]y=3[/latex]; a total of 7 units. We can find this number by subtracting the [latex]y[/latex]-coordinates: 3 – (–4) = 7. Consequently, the slope of the line is [latex]m=\frac{7}{14}=\frac{1}{2}[/latex].

Figure 1. Slope between 2 points.
Let’s now consider two arbitrary points on a line. Suppose the first point is designated [latex](x_1, y_1)[/latex] and the second point is [latex](x_2,y_2)[/latex]. The run is the difference in [latex]x[/latex]-values, [latex]x_2-x_1[/latex], and the rise is the difference in [latex]y[/latex]-values, [latex]y_2-y_1[/latex]. So the slope of the line between these two points is [latex]m=\frac{y_2-y_1}{x_2-x_1}[/latex] (see figure 2). It does not matter which point we designate as the first point or the second point. We will always get the same slope as long as we subtract from one point to the other in the same order.

Figure 2. Determining the slope between 2 points on a line.
The notation [latex]\Delta[/latex] is often used in mathematics to represent “change in”, so “change in y” can be denoted by [latex]\Delta y[/latex], and “change in [latex]x[/latex]” can be denoted [latex]\Delta x[/latex]. So, slope = [latex]m=\frac{\Delta y}{\Delta x}[/latex].
SLOPE
The slope between two points on a line [latex](x_1, y_1)[/latex] and [latex](x_2, y_2)[/latex] is found by the equation [latex]m=\frac{y_2-y_1}{x_2-x_1}=\frac{\Delta y}{\Delta x}[/latex].
If [latex]y=f(x)[/latex] is a linear function, the rate of change of the function = the slope of the line representing the function on a graph.
Example 1
If [latex]f\left(x\right)[/latex] is a linear function and [latex]\left(3,-2\right)[/latex] and [latex]\left(8,1\right)[/latex] are points on the graph of the function, find the slope of the graphed line. Is the graph of this function increasing, decreasing, or neither?
Solution
The coordinate pairs are [latex]\left(3,-2\right)[/latex] and [latex]\left(8,1\right)[/latex]. To find the slope we find the rate of change of the function between the two points.
[latex]m=\dfrac{\Delta y}{\Delta x}=\dfrac{1-\left(-2\right)}{8 - 3}=\dfrac{3}{5}[/latex]
The function is increasing because [latex]m>0[/latex].
Alternatively, changing the order in which we use the points:
[latex]m=\dfrac{\Delta y}{\Delta x}=\dfrac{-2-1}{3-8}=\dfrac{-3}{-5}=\dfrac{3}{5}[/latex]
Notice that we get the same solution since the order the points are referenced does not matter.
The following video shows examples of how to find the slope of a line passing through two points and then determines whether the line is increasing, decreasing or neither.
Try It 1
The graph of a linear function passes through the points (–2, 4) and (3, 1). FInd the slope of the graphed line and determine whether it is increasing, decreasing, or neither.
The next video shows an example where the increase in cost for producing solar panels is determined by two data points.
Try It 2
A gym charges a membership fee and a fixed monthly amount. For 3 months the total cost is $110. For 8 months, the total cost is $210. Calculate the monthly amount.
Review of Fractions
Since a slope is a fraction, it is inevitable that there will be some operations with fractions involved when finding the equation of a linear function. Let’s have a quick review on how we add, subtract, multiply and divide two fractions.
Addition and Subtraction
To add or subtract two fractions, the fractions must have a common denominator. If they do not, we have to build two equivalent fractions so that they have the same denominator. We use the least common multiple (LCM) of the denominators to achieve this. Doing this makes the fractions look different from the originals but they still have the same value. The reason for using the LCM is that it could help avoid complicated computation or further simplification.
Example 2
Add [latex]\dfrac{2}{3}+ \dfrac{4}{5}[/latex].
Solution
[latex]\begin{aligned}&\dfrac{2}{3} +\dfrac{4}{5}&&\text{The LCM of 3 and 5 is 15}\\\\&=\dfrac{2\color{blue}{\times5}}{3\color{blue}{\times5}}+ \dfrac{4\color{blue}{\times3}}{5\color{blue}{\times3}}&&\text{Multiply both the numerator and denominator by the same number}\\\\&=\dfrac{10}{15} +\dfrac{12}{15}\\\\&=\dfrac{10 +12}{15}&&\text{Add the numerators; keep the common denominator}\\\\&=\dfrac{22}{15}&&\text{Simplify}\end{aligned}[/latex]
How do we find the LCM? The LCM must include all of the factors among the denominators because the LCM is a common multiple. This implies that we will need to factor each denominator into its prime factorization, so that we know what factors the LCM must include.
Example 3
Determine the LCM:
- 6 and 35
- 24 and 36
Solution
1. We start by factoring 6 and 35:
[latex]\begin{aligned}6&= 2\cdot3\\35&=5\cdot7\end{aligned}[/latex]
The LCM must include the highest power of every factor from both numbers:
LCM = [latex]2\cdot3\cdot5\cdot7=210[/latex]
2. We start by factoring 24 and 36:
[latex]\begin{aligned}24&= 2^3\cdot3\\36&=2^2\cdot3^2\end{aligned}[/latex]
The LCM must include the highest power of every factor from both numbers:
LCM = [latex]2^3\cdot3^2=72[/latex]
Try It 3
Determine the LCM:
- 10 and 21
- 20 and 45
Try It 4
Subtract: [latex]\dfrac{3}{10}-\dfrac{4}{25}[/latex]
Multiplication and Division
To multiply fractions, we multiply the numerators and multiply the denominators. We can simplify by cancelling any common factors on the numerator and denominator to 1. To multiply a fraction by a whole number, we write the whole number as a fraction over 1.
Example 4
Multiply:
- [latex]\dfrac{4}{9}\cdot\dfrac{27}{16}[/latex]
- [latex]3\cdot\dfrac{2}{5}[/latex]
Solution
1.
[latex]\begin{aligned}\dfrac{4}{9}\cdot\dfrac{27}{16}&=\dfrac{4\cdot27}{9\cdot16}&&\text{Multiply straight across}\\&=\dfrac{1\;\;\cancel{4}\cdot\cancel{27}\;\;3}{1\;\;\cancel{9}\cdot\cancel{16}\;\;4}&&\text{Cancel common factors}\\&=\dfrac{3}{4}\end{aligned}[/latex]
2.
[latex]\begin{aligned}3\cdot\dfrac{2}{5}&=\dfrac{3}{1}\cdot\dfrac{2}{5}&&\text{Write 3 as }\frac{3}{1}\\&=\dfrac{3\cdot2}{1\cdot5}&&\text{Multiply straight across}\\&=\dfrac{6}{5}\end{aligned}[/latex]
Try It 5
Multiply:
- [latex]4\cdot\dfrac{5}{12}[/latex]
- [latex]-\dfrac{2}{15}\cdot\dfrac{9}{4}[/latex]
To divide two fractions, we multiply the first fraction by the reciprocal of the second fraction.
Example 5
Divide:
- [latex]\dfrac{12}{5}\div(-4)[/latex]
- [latex]\dfrac{10}{3}\div\dfrac{5}{9}[/latex]
Solution
[latex]\begin{aligned}\dfrac{12}{5}\div(-4)&=\dfrac{12}{5}\cdot\dfrac{-1}{4}&&\text{Turn division into multiplication by the reciprocal}\\&=\dfrac{12\cdot(-1)}{5\cdot4}&&\text{Multiply straight across}\\&=\dfrac{3\;\;\cancel{12}\cdot (-1)}{5\cdot\cancel{4}\;\;1}&&\text{Cancel common factors}\\&=\dfrac{-3}{5}\\&=-\dfrac{3}{5}\end{aligned}[/latex]
Try It 6
Divide:
- [latex]\dfrac{5}{6}\div15[/latex]
- [latex]-\dfrac{20}{9}\div\dfrac{25}{12}[/latex]
Determining Linear Functions
A linear function may be described by the slope-intercept form [latex]f(x) = mx + b[/latex], where [latex]m[/latex] is the rate of change of the function or the slope of the graphed function, and [latex]b[/latex] is the initial value or [latex]y[/latex]-coordinate of the [latex]y[/latex]-intercept. There are several different situations and conditions we may be given to determine the equation of the linear function.
Given a Slope and the y-intercept
If we are given the slope and the [latex]y[/latex]-intercept, we are given the value of [latex]m[/latex] and [latex]b[/latex]. This allows us to jump right to slope-intercept form to find the function. For example, if we are told that the slope of a line is 2 and the [latex]y[/latex]-intercept is (0, 1), then using slope-intercept form, [latex]f(x)=x+b[/latex], the linear function will be [latex]f(x) = 2x + 1[/latex].
Examples 6
Find the function whose graph is a line with:
- slope = 4 and [latex]y[/latex]-intercept = (0, 8).
- slope = [latex]\frac{4}{3}[/latex] and [latex]y[/latex]-intercept = (0, –5).
- slope = 0 and [latex]y[/latex]-intercept = (0, 3).
- slope = [latex]-\frac{5}{6}[/latex] and [latex]y[/latex]-intercept = (0, 0).
Solution
We are given [latex]m[/latex] and [latex]b[/latex] so can use slope-intercept form [latex]f(x)=mx+b[/latex] to find the function.
- [latex]m=4[/latex] and [latex]b=8[/latex]. Therefore, the function is [latex]f(x)=4x+8[/latex].
- [latex]m=\frac{4}{3}[/latex] and [latex]b=-5[/latex]. Therefore, the function is [latex]f(x)=\frac{4}{3}x-5[/latex].
- [latex]m=0[/latex] and [latex]b=3[/latex]. Therefore, the function is [latex]f(x)=0x+3[/latex], which simplifies to [latex]f(x)=3[/latex].
- [latex]m=-\frac{5}{6}[/latex] and [latex]b=0[/latex]. Therefore, the function is [latex]f(x)=-\frac{5}{6}x+0[/latex], which simplifies to[latex]f(x)=-\frac{5}{6}x[/latex].
Try It 7
Find the function whose graph is a line with:
- slope = –2 and [latex]y[/latex]-intercept = (0, 3).
- slope = [latex]\frac{2}{3}[/latex] and [latex]y[/latex]-intercept = (0, 0).
- slope = 0 and [latex]y[/latex]-intercept = (0, -7).
- slope = [latex]\frac{5}{4}[/latex] and [latex]y[/latex]-intercept = [latex]-\frac{7}{2}[/latex].
Given a Slope and a Point
If we are given a slope and a point, then we need to find the [latex]y[/latex]-intercept in order to determine the linear function [latex]f(x)=mx+b[/latex]. Since the given point [latex](x_1,y_1)[/latex] lies on the line, it is a solution of the linear function. We say that [latex](x_1,y_1)[/latex] satisfies the function. We can use this piece of information to solve for [latex]b[/latex] and determine the function.
For example, suppose we are told that the slope of a line is [latex]\dfrac{1}{3}[/latex] and the point (6, –1) lies on the line. We know that the function can be found using [latex]f(x)=mx+b[/latex]. Because [latex]m=\frac{1}{3}[/latex] the function must be:
[latex]f(x) = \frac{1}{3}x + b[/latex]
We now need to find the value of [latex]b[/latex] and we can use the given point (6, –1) to do this. Because (6, –1) satisfies the equation, [latex]f(6)=-1[/latex].
This means that:
[latex]\begin{equation}\begin{aligned} -1 &= \frac{1}{3} \cdot 6 + b\\-1 &= 2 + b\\-3 &= b \end{aligned}\end{equation}[/latex]
Now that we know [latex]m=\frac{1}{3}[/latex] and [latex]b=-3[/latex], we can write the linear function as [latex]f(x) = \frac{1}{3}x - 3[/latex].
Example 7
Find the function whose graph is a line with slope [latex]\frac{3}{4}[/latex] that passes through the point (–3, 1).
Solution
First we are told that [latex]m=\frac{3}{4}[/latex], so the function is [latex]f(x)=\large\frac{3}{4}x+b[/latex].
To find the value of [latex]b[/latex], we use the given point (–3, 1) which tells us that [latex]f(-3)=1[/latex].
[latex]\begin{equation}\begin{aligned}f(x)&=\frac{3}{4}x+b\\1&=\frac{3}{4}\cdot (-3) + b\\1&=-\frac{9}{4}+b\\1+\frac{9}{4}&=b\\ \frac{4}{4}+\frac{9}{4}&=b\\ \frac{13}{4}&=b\end{aligned}\end{equation}[/latex]
Now we know [latex]m[/latex] and [latex]b[/latex], the function is [latex]f(x)=\large\frac{3}{4}x+\frac{13}{4}[/latex]
Try It 8
Find the function whose graph is a line with slope –3 that passes through the point (4, –5).
Given Two Points
If we are given two points that lie on the graph of the function, then we have to find both the slope and the [latex]y[/latex]-intercept in order to determine the linear function. We can find the slope by finding the rate of change between the two points:
[latex]m=\dfrac{y_2 - y_1}{x_2 - x_1}[/latex]
After we find the slope, then we can use either one of the two points on the line to find the value of [latex]b[/latex] because both of the two points satisfy the linear function.
For example, given the two points (–1, 3) and (4, –7) that satisfy the function , the slope of the line representing the linear function will be:
Slope = [latex]m=\dfrac{-7-3}{4-(-1)} =\dfrac{-10}{5} = -2[/latex]
Since both point (–1, 3) and (4, –7) satisfy the function, we may use either of the two points. Let’s use the point (4, –7):
[latex]\begin{equation}\begin{aligned}f(x)&=-2x+b\\-7&=-2\cdot 4+b\\-7&=-8+b\\1&=b\end{aligned}\end{equation}[/latex]
We now know that [latex]m=-2[/latex] and [latex]b=1[/latex] so the linear function is [latex]f(x) = -2x + 1[/latex].
Example 8
Find the function whose graph is a line that passes through the points (–3, 5) and (4, –2).
Solution
FIrst we must find the slope of the line: [latex]m=\frac{\Delta y}{\Delta x}=\frac{-2-5}{4-(-3)}=\frac{-7}{7}=-1[/latex]
This means that the function is: [latex]f(x)=-x+b[/latex]
To find the value of [latex]b[/latex], we can use either point on the line that satisfies the function.
Let’s use (4, –2), which means [latex]f(4)=-2[/latex]:
[latex]\begin{equation}\begin{aligned}f(x)&=-x+b\\-2&=-(4)+b\\2&=b\end{aligned}\end{equation}[/latex]
Now we know that [latex]m=-1[/latex] and [latex]b=2[/latex] so we can write the function as [latex]f(x)=-x+2[/latex].
Try It 9
Find the function whose graph is a line that passes through the points (0, 5) and (–3, 8).
Given a Graph
If we are given a line on the coordinate plane, we may use any of the methods discussed above to find the function of the line by identifying the slope and the [latex]y[/latex]-intercept of the line, or the slope and a point on the line, or two points on the line.
Example 9
Find the function represented by the graph:

Solution
The [latex]y[/latex]-intercept is (0, –5) so we know that [latex]b=-5[/latex] in the function [latex]f(x)=mx+b[/latex].
To find the slope [latex]m[/latex], we use any other point on the line. Let’s use (5, 5):
[latex]m=\dfrac{\Delta y}{\Delta x}=\dfrac{5-(-5)}{5-0}=\dfrac{10}{5}=2[/latex]
Therefore, the function is [latex]f(x)=2x-5[/latex].
Example 10
Find the function represented by the graph:

Solution
The [latex]y[/latex]-intercept is fractional between [latex]y=[/latex] 1 and 2 and therefore not obvious, so we will use two points on the graph to find the function: (3, 0) and (–5, 4).
To find the slope:
[latex]m=\dfrac{\Delta y}{\Delta x}=\dfrac{4-0}{-5-3}=\dfrac{4}{-8}=-\dfrac{1}{2}[/latex].
The function can be written: [latex]f(x)=-\frac{1}{2}x+b[/latex]
To find [latex]b[/latex] we can use any point on the line. Let’s use (3, 0):
[latex]\begin{equation}\begin{aligned}f(x)&=-\frac{1}{2}x+b\\0&=-\frac{1}{2}\cdot 3+b\\0&=-\frac{3}{2}+b\\\frac{3}{2}=b\end{aligned}\end{equation}[/latex]
Now we know that [latex]m=-\frac{1}{2}[/latex] and [latex]b=\frac{3}{2}[/latex], so the function is [latex]f(x)=-\frac{1}{2}x+\frac{3}{2}[/latex]
Try It 10
Find the function represented by each graph:

Graph 1

Graph 2
If we are given a horizontal line, its slope is 0 because the rise is 0 (i.e., [latex]\dfrac{0}{run} = 0[/latex]). Sometimes we can identify the [latex]y[/latex]-intercept on the graph, and the function is [latex]f(x)=0x +b[/latex] or [latex]f(x)=b[/latex]. For example, for the function of the red horizontal line in figure 3, the [latex]y[/latex]-intercept is (0, 3) and therefore the function is [latex]f(x)=3[/latex].
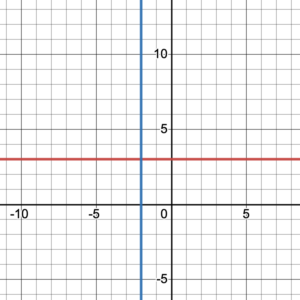
Figure 3. A horizontal line and a vertical line.
If we are given a vertical line, like the blue line in figure 3, it is not a function because a vertical line is a one-to-many mapping (i.e., one input with many different outputs). Therefore, we are not able to use the function form [latex]f(x)=mx+b[/latex] to express a vertical line. Also, the slope of a vertical line is undefined because the run is 0, and a number divided by 0 is undefined (i.e., [latex]\dfrac{rise}{0}[/latex] is undefined). The equation for a vertical line is [latex]x = a[/latex] where [latex]a[/latex] is the [latex]x[/latex]-coordinate of the [latex]x[/latex]-intercept. Indeed, for all of the points on a vertical line, the [latex]x[/latex]-coordinates are identical and the [latex]y[/latex]-coordinates are any real number on the vertical line. For example, the equation of the blue vertical line in figure 3 is [latex]x = -2[/latex].
Given a Point and a Parallel Linear Function
Finding the equation of a function whose graph is parallel to another line, still requires finding the slope and [latex]y[/latex]-intercept. Fortunately, the slope can be found from the parallel line since parallel lines have the same slope. Knowing the slope, we can then use another point on the line to determine the [latex]y[/latex]-intercept and consequently the function.
For example, suppose we are asked to find the linear function that passes through the point (8, –2), whose graph runs parallel to the graph of the function [latex]g(x)=\frac{3}{4}x+2[/latex]. The slope of the line that represents [latex]g(x)[/latex] is [latex]\frac{3}{4}[/latex]. This means that the line representing [latex]f(x)[/latex] also has a slope of [latex]\frac{3}{4}[/latex] since they are parallel. this means that [latex]f(x)=\frac{3}{4}x + b[/latex]. Now, we can find the value of [latex]b[/latex] by using the given point (8, –2):
[latex]\begin{equation}\begin{aligned}f(x)&=\frac{3}{4}x+b\\-2&=\frac{3}{4}\cdot 8+b\\-2&=6+b\\-8=b\end{aligned}\end{equation}[/latex]
Now we know that [latex]m=\frac{3}{4}[/latex] and [latex]b=-8[/latex]. Therefore, the function is [latex]f(x) = \frac{3}{4}x - 8[/latex].
Example 11
Find the function that is represented by a line that passes through the point (4, –2) and runs parallel to the line representing the function [latex]f(x)=3x-4[/latex].
Solution
The function [latex]f(x)=3x-4[/latex] is of the form [latex]f(x)=mx+b[/latex], so [latex]m=3[/latex].
The function we are trying to find is parallel to this so shares the same value of [latex]m[/latex].
We know that the line passes through (4, –2) with a slope of 2 so we can substitute this information into the function [latex]f(x)=mx+b[/latex] to find the value of [latex]b[/latex]:
[latex]f(x)=mx+b\\-2=3(4)+b\\-2=12+b\\-14=b[/latex]
Therefore, the function is [latex]f(x)=3x-14[/latex]
Try It 11
Find the function that is represented by a line that passes through the point (–5, 3) and runs parallel to the line representing the function [latex]f(x)=-4x+7[/latex].
Given a Point and a Perpendicular Linear Function
Determining the function whose graph passes through a given point and is perpendicular to the another function is found in a similar way to that of a given point and a parallel function. We must still determine the slope and [latex]y[/latex]-intercept of the function, Since the function is perpendicular to the given function, we know that the slopes are the negative reciprocals of each other.
For example, suppose we are asked to find the linear function whose graph passes through the point (–6, 1) and is perpendicular to the graph of the function [latex]g(x)=\frac{3}{4}x - 5[/latex]. The line represented by [latex]g(x)[/latex] has a slope of [latex]\frac{3}{4}[/latex]. This means that the line represented by [latex]f(x)[/latex] must have a slope of [latex]-\dfrac{4}{3}[/latex] because the lines are perpendicular.
Knowing the slope, we now have [latex]f(x) = -\frac{4}{3}x + b[/latex]. To find the value of [latex]b[/latex], we can use the point (–6, 1):
[latex]\begin{equation}\begin{aligned}f(x)&=-\frac{4}{3}x+b\\1&=-\frac{4}{3}\cdot (-6)+b\\1&=8+b\\-7&=b\end{aligned}\end{equation}[/latex]
Now that we know [latex]m=-\frac{4}{3}[/latex] and [latex]b=-7[/latex], we can write the linear function as [latex]f(x) = -\frac{4}{3}x - 7[/latex].
Example 12
Find the function that is represented by a line that passes through the point (–1, –3) and runs perpendicular to the line representing the function [latex]f(x)=4x-2[/latex].
Solution
The function [latex]f(x)=4x-2[/latex] is of the form [latex]f(x)=mx+b[/latex], so [latex]m=4[/latex].
The function we are trying to find is perpendicular to this so has an [latex]m[/latex]-value that is the negative reciprocal of 4: [latex]m=-\dfrac{1}{4}[/latex].
We now know that the line passes through (–1, –3) with a slope of[latex]-\frac{1}{4}[/latex] so we can substitute this information into the function [latex]f(x)=mx+b[/latex] to find the value of [latex]b[/latex]:
[latex]f(x)=mx+b\\-3=-\dfrac{1}{4}(-1)+b\\-3=\dfrac{1}{4}+b\\-\dfrac{12}{4}-\dfrac{1}{4}=b\\-\dfrac{13}{4}=b[/latex]
Therefore, the function is [latex]f(x)=-\dfrac{1}{4}x-\dfrac{13}{4}[/latex]
Try It 12
Find the function that is represented by a line that passes through the point (4, –6) and runs perpendicular to the line representing the function [latex]f(x)=\dfrac{3}{2}x-1[/latex].
Candela Citations
- Algebraic Analysis of Linear Functions. Authored by: Hazel McKenna and Leo Chang. Provided by: Utah Valley University. Located at: http://www.desmos.com/calculator. License: CC BY: Attribution
- All graphs created using desmos graphing calculator. Authored by: Hazel McKenna and Leo Chang. Provided by: Utah Valley University. License: CC BY: Attribution
- All Examples and Try Its. Authored by: Hazel McKenna. Provided by: Utah Valley University. License: CC BY: Attribution
- Ex: Find the Slope Given Two Points and Describe the Line. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/in3NTcx11I8. License: CC BY: Attribution
- Ex: Slope Application Involving Production Costs. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/4RbniDgEGE4. License: CC BY: Attribution
