Learning Outcomes
- Use the substitution method to find solution(s) to a system of two linear equations.
- Use the addition method to find solution(s) to a system of linear equations.
Solving Systems of Equations by Substitution
Solving a linear system in two variables by graphing works well when the solution consists of integer values, but if our solution contains decimals or fractions, it is not the most precise method. We will consider two more methods of solving a system of linear equations that are more precise than graphing. One such method is solving a system of equations by the substitution method, in which we solve one of the equations for one variable and then substitute the result into the second equation to solve for the second variable. Recall that we can solve for only one variable at a time, which is the reason the substitution method is both valuable and practical.
How To: Given a system of two equations in two variables, solve using the substitution method.
- Solve one of the two equations for one of the variables in terms of the other.
- Substitute the expression for this variable into the second equation, then solve for the remaining variable.
- Substitute that solution into either of the original equations to find the value of the first variable. If possible, write the solution as an ordered pair.
- Check the solution in both equations.
Example: Solving a System of Equations in Two Variables by Substitution
Solve the following system of equations by substitution.
[latex]\begin{align}-x+y&=-5 \\ 2x-5y&=1 \end{align}[/latex]
Try It
You can use an online graphing tool to help you solve a system of equations by substitution. We will use the following system to show you how:
[latex]\begin{align}x&=y+3 \\ 4&=3x - 2y \end{align}[/latex]
First, solve both equations for y:
[latex]\begin{align}y&=x-3 \\ y&=\frac{3}{2}x - 2 \end{align}[/latex]
Now enter [latex]x-3=\frac{3}{2}x - 2[/latex] into Desmos. You will see that Desmos has provided you with [latex]x = -2[/latex].
You now can substitute [latex]x = -2[/latex] into both equations. If you get the same result for both, you have found an ordered pair solution. Give it a try.
Q & A
Can the substitution method be used to solve any linear system in two variables?
Yes, but the method works best if one of the equations contains a coefficient of 1 or –1 so that we do not have to deal with fractions.
The following video is ~10 minutes long and provides a mini-lesson on using the substitution method to solve a system of linear equations. We present three different examples, and also use a graphing tool to help summarize the solution for each example.
Solving Systems of Equations in Two Variables by the Addition Method
A third method of solving systems of linear equations is the addition method, this method is also called the elimination method. In this method, we add two terms with the same variable, but opposite coefficients, so that the sum is zero. Of course, not all systems are set up with the two terms of one variable having opposite coefficients. Often we must adjust one or both of the equations by multiplication so that one variable will be eliminated by addition.
How To: Given a system of equations, solve using the addition method.
- Write both equations with x– and y-variables on the left side of the equal sign and constants on the right.
- Write one equation above the other, lining up corresponding variables. If one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, add the equations together, eliminating one variable. If not, use multiplication by a nonzero number so that one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, then add the equations to eliminate the variable.
- Solve the resulting equation for the remaining variable.
- Substitute that value into one of the original equations and solve for the second variable.
- Check the solution by substituting the values into the other equation.
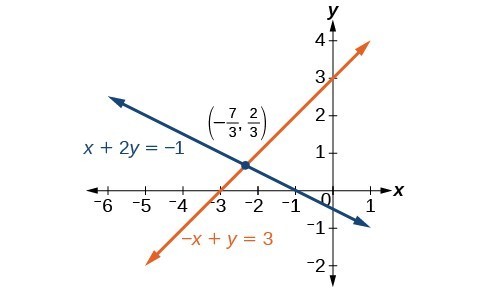
Example: Solving a System by the Addition Method
Solve the given system of equations by addition.
[latex]\begin{align}x+2y&=-1 \\ -x+y&=3 \end{align}[/latex]
Key Takeaways
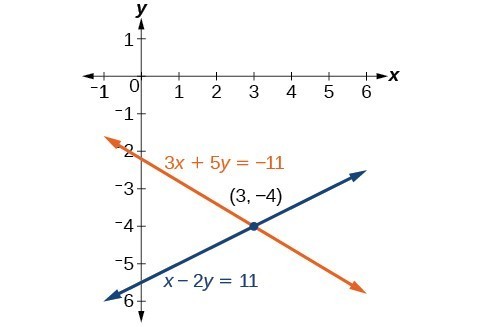
Example: Using the Addition Method When Multiplication of One Equation Is Required
Solve the given system of equations by the addition method.
[latex]\begin{align}3x+5y&=-11 \\ x - 2y&=11 \end{align}[/latex]
Try It
Solve the system of equations by addition.
[latex]\begin{align}2x - 7y&=2\\ 3x+y&=-20\end{align}[/latex]
Example: Using the Addition Method When Multiplication of Both Equations Is Required
Solve the given system of equations in two variables by addition.
[latex]\begin{align}2x+3y&=-16 \\ 5x - 10y&=30\end{align}[/latex]
Example: Using the Addition Method in Systems of Equations Containing Fractions
Solve the given system of equations in two variables by addition.
[latex]\begin{align}\frac{x}{3}+\frac{y}{6}&=3 \\[1mm] \frac{x}{2}-\frac{y}{4}&=1 \end{align}[/latex]
Try It
Solve the system of equations by addition.
[latex]\begin{align}2x+3y&=8\\ 3x+5y&=10\end{align}[/latex]
in the following video we present more examples of how to use the addition (elimination) method to solve a system of two linear equations.
Contribute!
Candela Citations
- Solving Systems of Equations using Elimination. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/ova8GSmPV4o. License: CC BY: Attribution
- Solving Systems of Equations using Substitution . Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/HxhacvH49o8. License: CC BY: Attribution
- Question ID 115164, 115120, 115110. Authored by: Shabazian, Roy. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL