Learning Outcomes
- Set up a linear equation involving distance, rate, and time.
- Find the dimensions of a rectangle given the area.
- Find the dimensions of a box given information about its side lengths.
Many applications are solved using known formulas. The problem is stated, a formula is identified, the known quantities are substituted into the formula, the equation is solved for the unknown, and the problem’s question is answered. Sometimes, these problems involve two equations representing two unknowns, which can be written using one equation in one variable by expressing one unknown in terms of the other. Examples of formulas include the perimeter of a rectangle, [latex]P=2L+2W[/latex]; the area of a rectangular region, [latex]A=LW[/latex]; and the volume of a rectangular solid, [latex]V=LWH[/latex].
Recall the relationship between distance, rate and time
The distance [latex]d[/latex] covered when traveling at a constant rate [latex]r[/latex] for some time [latex]t[/latex] is given by the formula [latex]d=rt[/latex].
Example: Solving an Application Using a Formula
It takes Andrew 30 minutes to drive to work in the morning. He drives home using the same route, but it takes 10 minutes longer, and he averages 10 mi/h less than in the morning. How far does Andrew drive to work?
Show Solution
This is a distance problem, so we can use the formula [latex]d=rt[/latex], where distance equals rate multiplied by time. Note that when rate is given in mi/h, time must be expressed in hours. Consistent units of measurement are key to obtaining a correct solution.
First, we identify the known and unknown quantities. Andrew’s morning drive to work takes 30 min, or [latex]\frac{1}{2}[/latex] h at rate [latex]r[/latex]. His drive home takes 40 min, or [latex]\frac{2}{3}[/latex] h, and his speed averages 10 mi/h less than the morning drive. Both trips cover distance [latex]d[/latex]. A table, such as the one below, is often helpful for keeping track of information in these types of problems.
|
[latex]d[/latex] |
[latex]r[/latex] |
[latex]t[/latex] |
| To Work |
[latex]d[/latex] |
[latex]r[/latex] |
[latex]\frac{1}{2}[/latex] |
| To Home |
[latex]d[/latex] |
[latex]r - 10[/latex] |
[latex]\frac{2}{3}[/latex] |
Write two equations, one for each trip.
[latex]\begin{array}{ll}d=r\left(\frac{1}{2}\right)\hfill & \text{To work}\hfill \\ d=\left(r - 10\right)\left(\frac{2}{3}\right)\hfill & \text{To home}\hfill \end{array}[/latex]
As both equations equal the same distance, we set them equal to each other and solve for r.
[latex]\begin{array}{c}r\left(\frac{1}{2}\right)=\left(r - 10\right)\left(\frac{2}{3}\right)\hfill \\ \frac{1}{2}r=\frac{2}{3}r-\frac{20}{3}\hfill \\ \frac{1}{2}r-\frac{2}{3}r=-\frac{20}{3}\hfill \\ -\frac{1}{6}r=-\frac{20}{3}\hfill \\ r=-\frac{20}{3}\left(-6\right)\hfill \\ r=40\hfill \end{array}[/latex]
We have solved for the rate of speed to work, 40 mph. Substituting 40 into the rate on the return trip yields 30 mi/h. Now we can answer the question. Substitute the rate back into either equation and solve for d.
[latex]\begin{array}{l}d\hfill&=40\left(\frac{1}{2}\right)\hfill \\ \hfill&=20\hfill \end{array}[/latex]
The distance between home and work is 20 mi.
Analysis of the Solution
Note that we could have cleared the fractions in the equation by multiplying both sides of the equation by the LCD to solve for [latex]r[/latex].
[latex]\begin{array}{l}r\left(\frac{1}{2}\right)=\left(r - 10\right)\left(\frac{2}{3}\right)\hfill \\ 6\times r\left(\frac{1}{2}\right)=6\times \left(r - 10\right)\left(\frac{2}{3}\right)\hfill \\ 3r=4\left(r - 10\right)\hfill \\ 3r=4r - 40\hfill \\ -r=-40\hfill \\ r=40\hfill \end{array}[/latex]
How were the fractions handled in the example above?
Recall that when solving multi-step equations, it is helpful to multiply by the LCD to clear the denominators from the equation.
But it is also permissible to use operations on fractions to combine like terms. The example above demonstrates both.
more
- In the text of the solution when solving for [latex]r[/latex] the first time, the parentheses were eliminated using the distributive property, then operations on fractions were used to combine like terms.
[latex]\begin{array}{c}r\left(\frac{1}{2}\right)=\left(r - 10\right)\left(\frac{2}{3}\right)\hfill \\ \frac{1}{2}r=\frac{2}{3}r-\frac{20}{3}\hfill \\ \frac{1}{2}r-\frac{2}{3}r=-\frac{20}{3}\hfill \\ -\frac{1}{6}r=-\frac{20}{3}\hfill \\ r=-\frac{20}{3}\left(-6\right)\hfill \\ r=40\hfill \end{array}[/latex]
- Later, in the analysis of the solution, the LCD between the denominators [latex]2 \text{ and } 3 [/latex] was multiplied on both sides of the equation to cancel out the denominators so that operations on fractions were not necessary. Do you see how the LCD wasn’t actually multiplied through on both sides, but that the denominators cancelled out, resulting in a linear equation in one variable without denominators?
[latex]\begin{array}{l}r\left(\frac{1}{2}\right)=\left(r - 10\right)\left(\frac{2}{3}\right)\hfill \\ 6\times r\left(\frac{1}{2}\right)=6\times \left(r - 10\right)\left(\frac{2}{3}\right)\hfill \\ 3r=4\left(r - 10\right)\hfill \\ 3r=4r - 40\hfill \\ -r=-40\hfill \\ r=40\hfill \end{array}[/latex]
Both methods are equally correct unless your instructor requires you to specifically demonstrate knowledge of one or the other.
Which do you prefer?
How To: Solve Multi-Step Equations
1. (Optional) Multiply to clear any fractions or decimals.
2. Simplify each side by clearing parentheses and combining like terms.
3. Add or subtract to isolate the variable term—you may have to move a term with the variable.
4. Multiply or divide to isolate the variable.
5. Check the solution.
Try It
On Saturday morning, it took Jennifer 3.6 hours to drive to her mother’s house for the weekend. On Sunday evening, due to heavy traffic, it took Jennifer 4 hours to return home. Her speed was 5 mi/h slower on Sunday than on Saturday. What was her speed on Sunday?
Show Solution
45 [latex]\frac{\text{mi}}{\text{h}}[/latex]
Example: Solving a Perimeter Problem
The perimeter of a rectangular outdoor patio is [latex]54[/latex] ft. The length is [latex]3[/latex] ft. greater than the width. What are the dimensions of the patio?
Show Solution
The perimeter formula is standard: [latex]P=2L+2W[/latex]. We have two unknown quantities, length and width. However, we can write the length in terms of the width as [latex]L=W+3[/latex]. Substitute the perimeter value and the expression for length into the formula. It is often helpful to make a sketch and label the sides as shown below.
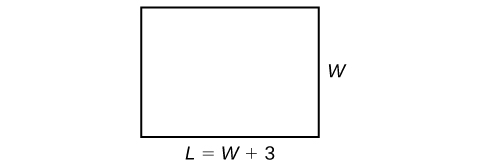
Now we can solve for the width and then calculate the length.
[latex]\begin{array}{l}P=2L+2W\hfill \\ 54=2\left(W+3\right)+2W\hfill \\ 54=2W+6+2W\hfill \\ 54=4W+6\hfill \\ 48=4W\hfill \\ 12=W\hfill \\ \left(12+3\right)=L\hfill \\ 15=L\hfill \end{array}[/latex]
The dimensions are [latex]L=15[/latex] ft and [latex]W=12[/latex] ft.
Evaluating a variable for an expression
In the example above, the length was written in terms of the width in order to substitute it for the variable [latex]L[/latex] to be able to write one equation in one variable.
This is a powerful technique in algebra and should be practiced until it becomes familiar, so it’s worth taking a closer look.
more
We had [latex]P = 2L + 2W[/latex], which is one equation in two variables. Given the value for [latex]P[/latex], we don’t have enough information to solve for either [latex]L[/latex] or [latex]W[/latex].
But we do know that [latex]L=W+3[/latex]. We can use this to substitute for the [latex]L[/latex] in the original equation. Be careful to retain the original statement exactly, substituting only the value for [latex]L[/latex]. A handy way to handle the substitution is with a set of parentheses.
[latex]\begin{array}{l}P=2L+2W\hfill \\ 54=2\left(L\right)+2W \,\,\,\,\,\,\,\, \text{ wrap the } L \text{ to see where to make the substitution} \hfill \\ 54=2\left(W+3\right)+2W \,\,\,\,\, \text{ drop the expression for } L \text{ into the parentheses}\hfill \\ 54=2W+6+2W\hfill \\ 54=4W+6\end{array}[/latex]
Now we have one equation in one variable. We can use the properties of equality to isolate the variable [latex]W[/latex] on one side, with its numerical value on the other.
Try It
Find the dimensions of a rectangle given that the perimeter is [latex]110[/latex] cm. and the length is 1 cm. more than twice the width.
Example: Solving an Area Problem
The perimeter of a tablet of graph paper is 48 in2. The length is [latex]6[/latex] in. more than the width. Find the area of the graph paper.
Show Solution
The standard formula for area is [latex]A=LW[/latex]; however, we will solve the problem using the perimeter formula. The reason we use the perimeter formula is because we know enough information about the perimeter that the formula will allow us to solve for one of the unknowns. As both perimeter and area use length and width as dimensions, they are often used together to solve a problem such as this one.
We know that the length is 6 in. more than the width, so we can write length as [latex]L=W+6[/latex]. Substitute the value of the perimeter and the expression for length into the perimeter formula and find the length.
[latex]\begin{array}{l}P=2L+2W\hfill \\ 48=2\left(W+6\right)+2W\hfill \\ 48=2W+12+2W\hfill \\ 48=4W+12\hfill \\ 36=4W\hfill \\ 9=W\hfill \\ \left(9+6\right)=L\hfill \\ 15=L\hfill \end{array}[/latex]
Now, we find the area given the dimensions of [latex]L=15[/latex] in. and [latex]W=9[/latex] in.
[latex]\begin{array}{l}A\hfill&=LW\hfill \\ A\hfill&=15\left(9\right)\hfill \\ \hfill&=135\text{ in}^{2}\hfill \end{array}[/latex]
The area is [latex]135[/latex] in2.
Try It
A game room has a perimeter of 70 ft. The length is five more than twice the width. How many ft2 of new carpeting should be ordered?
Example: Solving a Volume Problem
Find the dimensions of a shipping box given that the length is twice the width, the height is [latex]8[/latex] inches, and the volume is 1,600 in.3.
Show Solution
The formula for the volume of a box is given as [latex]V=LWH[/latex], the product of length, width, and height. We are given that [latex]L=2W[/latex], and [latex]H=8[/latex]. The volume is [latex]1,600[/latex] cubic inches.
[latex]\begin{array}{l}V=LWH \\ 1,600=\left(2W\right)W\left(8\right) \\ 1,600=16{W}^{2} \\ 100={W}^{2} \\ 10=W \end{array}[/latex]
The dimensions are [latex]L=20[/latex] in., [latex]W=10[/latex] in., and [latex]H=8[/latex] in.
Analysis of the Solution
Note that the square root of [latex]{W}^{2}[/latex] would result in a positive and a negative value. However, because we are describing width, we can use only the positive result.

