Adding and Subtracting Fractions

Learning OUTCOMES

Use addition and subtraction when evaluating expressions with fractions

Addition and Subtraction of Fractions with Common Denominators

How many quarters are pictured below?

Three U.S. quarters are shown. One is shown on the left, and two are shown on the right.

You can quickly count three, but if you look carefully the image represents $1$ quarter plus $2$ quarters equals $3$ quarters.

Remember, quarters are really fractions of a dollar. Quarters are another way to say fourths. So the picture of the coins shows that

${\Large\frac{1}{4}}+{\Large\frac{2}{4}}=\Large{\frac{3}{4}}$

$\text{one quarter }+\text{ two quarters }=\text{ three quarters}$

Let’s use fraction circles to model the same example, $\Large\frac{1}{4}\normalsize+\Large\frac{2}{4}$ .

Start with one $\Large\frac{1}{4}$ piece.		$\Large\frac{1}{4}$
Add two more $\Large\frac{1}{4}$ pieces.		$+\Large\frac{2}{4}$
The result is $\Large\frac{3}{4}$ .		$\Large\frac{3}{4}$

So again, we see that

$\Large\frac{1}{4}\normalsize+\Large\frac{2}{4}\normalsize=\Large\frac{3}{4}$

example

Use a model to find the sum $\Large\frac{3}{8}\normalsize+\Large\frac{2}{8}$ .

Solution:

Start with three $\Large\frac{1}{8}$ pieces.		$\Large\frac{3}{8}$
Add two $\Large\frac{1}{8}$ pieces.		$+\Large\frac{2}{8}$
How many $\Large\frac{1}{8}$ pieces are there?		$\Large\frac{5}{8}$

There are five $\Large\frac{1}{8}$ pieces, or five-eighths. The model shows that $\Large\frac{3}{8}\normalsize+\Large\frac{2}{8}\normalsize=\Large\frac{5}{8}$ .

try it

Use a model to find each sum. Show a diagram to illustrate your model.

$\Large\frac{1}{8}\normalsize+\Large\frac{4}{8}$

Show Answer

$\frac{5}{8}$

A circle divided into 8 sections, 5 of which are shaded.

Use a model to find each sum. Show a diagram to illustrate your model.
$\Large\frac{1}{6}\normalsize+\Large\frac{4}{6}$

Show Answer

$\frac{5}{6}$

A circle divided into 6 sections, 5 of which are shaded.

The following video shows more examples of how to use models to add fractions with like denominators (the value in the lower part of a fraction that represents how many equal parts a whole has been divided into).

Subtracting two fractions with common denominators follows the same process as adding fractions with common denominators. Think of a pizza that was cut into $12$ slices. Suppose five pieces are eaten for dinner. This means that, after dinner, there are seven pieces (or ${\Large\frac{7}{12}}$ of the pizza) left in the box. If Leonardo eats $2$ of these remaining pieces (or ${\Large\frac{2}{12}}$ of the pizza), how much is left? There would be $5$ pieces left (or ${\Large\frac{5}{12}}$ of the pizza).

${\Large\frac{7}{12}}-{\Large\frac{2}{12}}={\Large\frac{5}{12}}$

Let’s use fraction circles to model the same example, ${\Large\frac{7}{12}}-{\Large\frac{2}{12}}$ .

Start with seven ${\Large\frac{1}{12}}$ pieces. Take away two ${\Large\frac{1}{12}}$ pieces. How many twelfths are left?

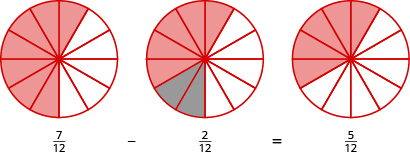
The bottom reads 7 twelfths minus 2 twelfths equals 5 twelfths. Above 7 twelfths, there is a circle divided into 12 equal pieces, with 7 pieces shaded in orange. Above 2 twelfths, the same circle is shown, but 2 of the 7 pieces are shaded in grey. Above 5 twelfths, the 2 grey pieces are no longer shaded, so there is a circle divided into 12 pieces with 5 of the pieces shaded in orange.
Again, we have five twelfths, ${\Large\frac{5}{12}}$ .

Example

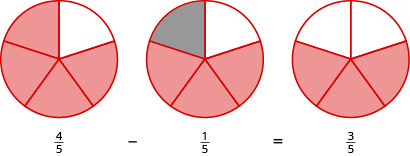
Use fraction circles to find the difference: ${\Large\frac{4}{5}}-{\Large\frac{1}{5}}$

Solution:
Start with four ${\Large\frac{1}{5}}$ pieces. Take away one ${\Large\frac{1}{5}}$ piece. Count how many fifths are left. There are three ${\Large\frac{1}{5}}$ pieces left, or ${\Large\frac{3}{5}}$ of the circle left.

The bottom reads 4 fifths minus 1 fifth equals 3 fifths. Above 4 fifths, there is a circle divided into 5 equal pieces, with 4 pieces shaded in orange. Above 1 fifth, the same circle is shown, but 1 of the 4 shaded pieces is shaded in grey. Above 3 fifths, the 1 grey piece is no longer shaded, so there is a circle divided into 5 pieces with 3 of the pieces shaded in orange.

Try It

The examples above show that to add or subtract the same-size pieces—meaning that the fractions have the same denominator—we just add or subtract the number of pieces.

Fraction Addition

If $a,b,\text{ and }c$ are numbers where $c\ne 0$ , then

$\Large\frac{a}{c}\normalsize+\Large\frac{b}{c}\normalsize=\Large\frac{a+b}{c}$

To add fractions with a common denominators, add the numerators and place the sum over the common denominator.

Fraction Subtraction

If $a,b,\text{ and }c$ are numbers where $c\ne 0$ , then

${\Large\frac{a}{c}}-{\Large\frac{b}{c}}={\Large\frac{a-b}{c}}$

To subtract fractions with a common denominators, subtract the numerators and place the difference over the common denominator.

Example

Find the difference: ${\Large\frac{23}{24}}-{\Large\frac{14}{24}}$

Show Answer

Solution:

${\Large\frac{23}{24}}-{\Large\frac{14}{24}}$
Subtract the numerators and place the difference over the common denominator.	${\Large\frac{23 - 14}{24}}$
Simplify the numerator.	${\Large\frac{9}{24}}$
Simplify the fraction by removing common factors.	${\Large\frac{3}{8}}$

Try It

Now lets do an example that involves both addition and subtraction.

Example

Simplify: ${\Large\frac{3}{8}}+\left({\Large\frac{7}{8}}\right)-{\Large\frac{5}{8}}$

Show Answer

Solution:

	$\Large\frac{3}{8}+\left(\frac{7}{8}\right)-\frac{5}{8}$
Combine the numerators over the common denominator.	${\Large\frac{3+\left(7\right)-5}{8}}$
Simplify the numerator, working left to right.	${\Large\frac{10 - 5}{8}}$
Subtract the terms in the numerator.	${\Large\frac{5}{8}}$

Try It

Addition and Subtraction of Fractions with Different Denominators

We just reviewed how to add and subtract fractions with common denominators. But how can we add and subtract fractions with unlike denominators?

Let’s think about coins again. Can you add one quarter and one dime? You could say there are two coins, but that’s not very useful. To find the total value of one quarter plus one dime, you change them to the same kind of unit—cents. One quarter equals $25$ cents and one dime equals $10$ cents, so the sum is $35$ cents. See the image below.

Together, a quarter and a dime are worth $35$ cents, or ${\Large\frac{35}{100}}$ of a dollar.

A quarter and a dime are shown. Below them, it reads 25 cents plus 10 cents. Below that, it reads 35 cents.
Similarly, when we add fractions with different denominators we have to convert them to equivalent fractions with a common denominator. With the coins, when we convert to cents, the denominator is $100$ . Since there are $100$ cents in one dollar, $25$ cents is $\Large\frac{25}{100}$ and $10$ cents is $\Large\frac{10}{100}$ . So we add $\Large\frac{25}{100}+\Large\frac{10}{100}$ to get $\Large\frac{35}{100}$ , which is $35$ cents.

You have practiced adding and subtracting fractions with common denominators. Now let’s see what you need to do with fractions that have different denominators.

First, we will use fraction tiles to model finding the common denominator of $\Large\frac{1}{2}$ and $\Large\frac{1}{3}$ .

We’ll start with one $\Large\frac{1}{2}$ tile and $\Large\frac{1}{3}$ tile. We want to find a common fraction tile that we can use to match both $\Large\frac{1}{2}$ and $\Large\frac{1}{3}$ exactly.
If we try the $\Large\frac{1}{4}$ pieces, $2$ of them exactly match the $\Large\frac{1}{2}$ piece, but they do not exactly match the $\Large\frac{1}{3}$ piece.

Two rectangles are shown side by side. The first is labeled 1 half. The second is shorter and is labeled 1 third. Underneath the first rectangle is an equally sized rectangle split vertically into two pieces, each labeled 1 fourth. Underneath the second rectangle are two pieces, each labeled 1 fourth. These rectangles together are longer than the rectangle labeled as 1 third.
If we try the $\Large\frac{1}{5}$ pieces, they do not exactly cover the $\Large\frac{1}{2}$ piece or the $\Large\frac{1}{3}$ piece.

Two rectangles are shown side by side. The first is labeled 1 half. The second is shorter and is labeled 1 third. Underneath the first rectangle is an equally sized rectangle split vertically into three pieces, each labeled 1 sixth. Underneath the second rectangle is an equally sized rectangle split vertically into 2 pieces, each labeled 1 sixth.
If we try the $\Large\frac{1}{6}$ pieces, we see that exactly $3$ of them cover the $\Large\frac{1}{2}$ piece, and exactly $2$ of them cover the $\Large\frac{1}{3}$ piece.

If we were to try the $\Large\frac{1}{12}$ pieces, they would also work.

Two rectangles are shown side by side. The first is labeled 1 half. The second is shorter and is labeled 1 third. Underneath the first rectangle is an equally sized rectangle split vertically into 6 pieces, each labeled 1 twelfth. Underneath the second rectangle is an equally sized rectangle split vertically into 4 pieces, each labeled 1 twelfth.
Even smaller tiles, such as $\Large\frac{1}{24}$ and $\Large\frac{1}{48}$ , would also exactly cover the $\Large\frac{1}{2}$ piece and the $\Large\frac{1}{3}$ piece.

The denominator of the largest piece that covers both fractions is the least common denominator (LCD) of the two fractions. So, the least common denominator of $\Large\frac{1}{2}$ and $\Large\frac{1}{3}$ is $6$ .

Notice that all of the tiles that cover $\Large\frac{1}{2}$ and $\Large\frac{1}{3}$ have something in common: Their denominators are common multiples of $2$ and $3$ , the denominators of $\Large\frac{1}{2}$ and $\Large\frac{1}{3}$ . The least common multiple (LCM) of the denominators is $6$ , and so we say that $6$ is the least common denominator (LCD) of the fractions $\Large\frac{1}{2}$ and $\Large\frac{1}{3}$ .

Least Common Denominator

The least common denominator (LCD) of two fractions is the least common multiple (LCM) of their denominators.

To find the LCD of two fractions, we will find the LCM of their denominators. We follow the procedure we used earlier to find the LCM of two numbers. We only use the denominators of the fractions, not the numerators, when finding the LCD.

Example

Find the LCD for the fractions: $\Large\frac{7}{12}$ and $\Large\frac{5}{18}$

Solution:

Factor each denominator into its primes.
List the primes of $12$ and the primes of $18$ lining them up in columns when possible.
Bring down the columns.
Multiply the factors. The product is the LCM.	$\text{LCM}=36$
The LCM of $12$ and $18$ is $36$ , so the LCD of $\Large\frac{7}{12}$ and $\Large\frac{5}{18}$ is 36.	LCD of $\Large\frac{7}{12}$ and $\Large\frac{5}{18}$ is 36.

Try it

To find the LCD of two fractions, find the LCM of their denominators. Notice how the steps shown below are similar to the steps we took to find the LCM.

Find the least common denominator (LCD) of two fractions

Factor each denominator into its primes.
List the primes, matching primes in columns when possible.
Bring down the columns.
Multiply the factors. The product is the LCM of the denominators.
The LCM of the denominators is the LCD of the fractions.

Example

Find the least common denominator for the fractions: $\Large\frac{8}{15}$ and $\Large\frac{11}{24}$

Show Answer

Solution:
To find the LCD, we find the LCM of the denominators.
Find the LCM of $15$ and $24$ .

The top line shows 15 equals 3 times 5. The next line shows 24 equals 2 times 2 times 2 times 3. The 3s are lined up vertically. The next line shows LCM equals 2 times 2 times 2 times 3 times 5. The last line shows LCM equals 120.
The LCM of $15$ and $24$ is $120$ . So, the LCD of $\Large\frac{8}{15}$ and $\Large\frac{11}{24}$ is $120$ .

Try It

Earlier, we used fraction tiles to see that the LCD of $\Large\frac{1}{4}\normalsize\text{and}\Large\frac{1}{6}$ is $12$ . We saw that three $\Large\frac{1}{12}$ pieces exactly covered $\Large\frac{1}{4}$ and two $\Large\frac{1}{12}$ pieces exactly covered $\Large\frac{1}{6}$ , so

$\Large\frac{1}{4}=\Large\frac{3}{12}\normalsize\text{ and }\Large\frac{1}{6}=\Large\frac{2}{12}$ .

On the left is a rectangle labeled 1 fourth. Below it is an identical rectangle split vertically into 3 equal pieces, each labeled 1 twelfth. On the right is a rectangle labeled 1 sixth. Below it is an identical rectangle split vertically into 2 equal pieces, each labeled 1 twelfth.
We say that $\Large\frac{1}{4}\normalsize\text{ and }\Large\frac{3}{12}$ are equivalent fractions and also that $\Large\frac{1}{6}\normalsize\text{ and }\Large\frac{2}{12}$ are equivalent fractions.

We can use the Equivalent Fractions Property to algebraically change a fraction to an equivalent one. Remember, two fractions are equivalent if they have the same value. The Equivalent Fractions Property is repeated below for reference.

Equivalent Fractions Property

If $a,b,c$ are whole numbers where $b\ne 0,c\ne 0,\text{then}$

$\Large\frac{a}{b}=\Large\frac{a\cdot c}{b\cdot c}\normalsize\text{ and }\Large\frac{a\cdot c}{b\cdot c}=\Large\frac{a}{b}$

To add or subtract fractions with different denominators, we will first have to convert each fraction to an equivalent fraction with the LCD. Let’s see how to change $\Large\frac{1}{4}\normalsize\text{ and }\Large\frac{1}{6}$ to equivalent fractions with denominator $12$ without using models.

Example

Convert $\Large\frac{1}{4}\normalsize\text{ and }\Large\frac{1}{6}$ to equivalent fractions with denominator $12$ , their LCD.

Solution:

Find the LCD.	The LCD of $\Large\frac{1}{4}$ and $\Large\frac{1}{6}$ is $12$ .
Find the number to multiply $4$ to get $12$ .	$4\cdot\color{red}{3}=12$
Find the number to multiply $6$ to get $12$ .	$6\cdot\color{red}{2}=12$
Use the Equivalent Fractions Property to convert each fraction to an equivalent fraction with the LCD, multiplying both the numerator and denominator of each fraction by the same number.	$\Large\frac{1}{4}$ $\Large\frac{1}{6}$ $\Large\frac{1\cdot\color{red}{3}}{4\cdot\color{red}{3}}$ $\Large\frac{1\cdot\color{red}{2}}{6\cdot\color{red}{2}}$
Simplify the numerators and denominators.	$\Large\frac{3}{12}$ $\Large\frac{2}{12}$

We do not reduce the resulting fractions. If we did, we would get back to our original fractions and lose the common denominator.

Try it

Convert two fractions to equivalent fractions with their LCD as the common denominator

Find the LCD.
For each fraction, determine the number needed to multiply the denominator to get the LCD.
Use the Equivalent Fractions Property to multiply both the numerator and denominator by the number you found in Step 2.
Simplify the numerator and denominator.

Example

Convert $\Large\frac{8}{15}$ and $\Large\frac{11}{24}$ to equivalent fractions with denominator $120$ , their LCD.

Show Answer

Solution:

The LCD is $120$ . We will start at Step 2.
Find the number that must multiply $15$ to get $120$ .	$15\cdot\color{red}{8}=120$
Find the number that must multiply $24$ to get $120$ .	$24\cdot\color{red}{5}=120$
Use the Equivalent Fractions Property.	$\Large\frac{8\cdot\color{red}{8}}{15\cdot\color{red}{8}}$ $\Large\frac{11\cdot\color{red}{5}}{24\cdot\color{red}{5}}$
Simplify the numerators and denominators.	$\Large\frac{64}{120}$ $\Large\frac{55}{120}$

Try it

In our next video we show two more examples of how to use the column method to find the least common denominator of two fractions.

Once we have converted two fractions to equivalent forms with common denominators, we can add or subtract them by adding or subtracting the numerators.

Add or subtract fractions with different denominators

Find the LCD.
Convert each fraction to an equivalent form with the LCD as the denominator.
Add or subtract the fractions.
Write the result in simplified form.

Example

Add: $\Large\frac{1}{2}+\Large\frac{1}{3}$

Solution:

	$\Large\frac{1}{2}+\Large\frac{1}{3}$
Find the LCD of $2$ , $3$ .
Change into equivalent fractions with the LCD $6$ .	$\Large\frac{1\cdot\color{red}{3}}{2\cdot\color{red}{3}} +\Large\frac{1\cdot\color{red}{2}}{3\cdot\color{red}{2}}$
Simplify the numerators and denominators.	$\Large\frac{3}{6}+\Large\frac{2}{6}$
Add.	$\Large\frac{5}{6}$

Remember, always check to see if the answer can be simplified. Since $5$ and $6$ have no common factors, the fraction $\Large\frac{5}{6}$ cannot be reduced.

Try It

Watch the following video to see more examples and explanation about how to add two fractions with unlike denominators.

Example

Add: $\Large\frac{7}{12}+\Large\frac{5}{18}$

Show Answer

Solution:

	$\Large\frac{7}{12}+\Large\frac{5}{18}$
Find the LCD of $12$ and $18$ .
Rewrite as equivalent fractions with the LCD.	$\Large\frac{7\cdot\color{red}{3}}{12\cdot\color{red}{3}} +\Large\frac{5\cdot\color{red}{2}}{18\cdot\color{red}{2}}$
Simplify the numerators and denominators.	$\Large\frac{21}{36}+\Large\frac{10}{36}$
Add.	$\Large\frac{31}{36}$

Because $31$ is a prime number, it has no factors in common with $36$ . The answer is simplified.

Try It

The following video provides two more examples of how to subtract two fractions with unlike denominators.

Module 1: Whole Numbers, Fractions, Decimals, Percents and Problem Solving

Learning OUTCOMES

Addition and Subtraction of Fractions with Common Denominators

example

try it

Example

Try It

Fraction Addition

Fraction Subtraction

Example

Try It

Example

Try It

Addition and Subtraction of Fractions with Different Denominators

Least Common Denominator

Example

Try it

Find the least common denominator (LCD) of two fractions

Example

Try It

Equivalent Fractions Property

Example

Try it

Convert two fractions to equivalent fractions with their LCD as the common denominator

Example

Try it

Add or subtract fractions with different denominators

Example

Try It

Example

Try It

Try It

Try It

Candela Citations