Practice Makes Perfect

Use the Properties of Angles
In the following exercises, find ⓐ the supplement and ⓑ the complement of the given angle.

[latex]{53^\circ }[/latex]

ⓐ 127°
ⓑ 37°

[latex]{16^\circ }[/latex]

[latex]{29^\circ }[/latex]

ⓐ 151°
ⓑ 61°

[latex]{72^\circ }[/latex]

In the following exercises, use the properties of angles to solve.

Find the supplement of a [latex]{135^\circ }[/latex] angle.

45°

Find the complement of a [latex]{38^\circ }[/latex] angle.

Find the complement of a [latex]27.5^\circ [/latex] angle.

62.5°

Find the supplement of a [latex]109.5^\circ [/latex] angle.

Two angles are supplementary. The larger angle is [latex]{56^\circ }[/latex] more than the smaller angle. Find the measures of both angles.

62°, 118°

Two angles are supplementary. The smaller angle is [latex]{36^\circ }[/latex] less than the larger angle. Find the measures of both angles.

Two angles are complementary. The smaller angle is [latex]{34^\circ }[/latex] less than the larger angle. Find the measures of both angles.

62°, 28°

Two angles are complementary. The larger angle is [latex]{52^\circ }[/latex] more than the smaller angle. Find the measures of both angles.

Use the Properties of Triangles In the following exercises, solve using properties of triangles.

The measures of two angles of a triangle are [latex]{26^\circ }[/latex] and [latex]{98^\circ }[/latex]. Find the measure of the third angle.

56°

The measures of two angles of a triangle are [latex]{61^\circ }[/latex] and [latex]{84^\circ }[/latex]. Find the measure of the third angle.

The measures of two angles of a triangle are [latex]{105^\circ }[/latex] and [latex]{31^\circ }[/latex]. Find the measure of the third angle.

44°

The measures of two angles of a triangle are [latex]{47^\circ }[/latex] and [latex]{72^\circ }[/latex]. Find the measure of the third angle.

One angle of a right triangle measures [latex]{33^\circ }[/latex]. What is the measure of the other angle?

57°

One angle of a right triangle measures [latex]{51^\circ }[/latex]. What is the measure of the other angle?

One angle of a right triangle measures [latex]22.5^\circ [/latex]. What is the measure of the other angle?

67.5°

One angle of a right triangle measures [latex]36.5^\circ [/latex]. What is the measure of the other angle?

The two smaller angles of a right triangle have equal measures. Find the measures of all three angles.

45°, 45°, 90°

The measure of the smallest angle of a right triangle is [latex]{20^\circ }[/latex] less than the measure of the other small angle. Find the measures of all three angles.

The angles in a triangle are such that the measure of one angle is twice the measure of the smallest angle, while the measure of the third angle is three times the measure of the smallest angle. Find the measures of all three angles.

30°, 60°, 90°

The angles in a triangle are such that the measure of one angle is [latex]{20^\circ }[/latex] more than the measure of the smallest angle, while the measure of the third angle is three times the measure of the smallest angle. Find the measures of all three angles.

Find the Length of the Missing Side In the following exercises, [latex]\Delta ABC[/latex] is similar to [latex]\Delta XYZ[/latex]. Find the length of the indicated side.

side [latex]b[/latex]

12

side [latex]x[/latex]

On a map, San Francisco, Las Vegas, and Los Angeles form a triangle whose sides are shown in the figure below. The actual distance from Los Angeles to Las Vegas is [latex]270[/latex] miles.

Find the distance from Los Angeles to San Francisco.

351 miles

Find the distance from San Francisco to Las Vegas.

Use the Pythagorean Theorem In the following exercises, use the Pythagorean Theorem to find the length of the hypotenuse.

15

25

Find the Length of the Missing Side In the following exercises, use the Pythagorean Theorem to find the length of the missing side. Round to the nearest tenth, if necessary.

8

12

10.2

8

In the following exercises, solve. Approximate to the nearest tenth, if necessary.

A [latex]\text{13-foot}[/latex] string of lights will be attached to the top of a [latex]\text{12-foot}[/latex] pole for a holiday display. How far from the base of the pole should the end of the string of lights be anchored?

5 feet

Pam wants to put a banner across her garage door to congratulate her son on his college graduation. The garage door is [latex]12[/latex] feet high and [latex]16[/latex] feet wide. How long should the banner be to fit the garage door?

Chi is planning to put a path of paving stones through her flower garden. The flower garden is a square with sides of [latex]10[/latex] feet. What will the length of the path be?

14.1 feet

Brian borrowed a [latex]\text{20-foot}[/latex] extension ladder to paint his house. If he sets the base of the ladder [latex]6[/latex] feet from the house, how far up will the top of the ladder reach?

Everyday Math

Building a scale model Joe wants to build a doll house for his daughter. He wants the doll house to look just like his house. His house is [latex]30[/latex] feet wide and [latex]35[/latex] feet tall at the highest point of the roof. If the dollhouse will be [latex]2.5[/latex] feet wide, how tall will its highest point be?

2.9 feet

Measurement A city engineer plans to build a footbridge across a lake from point [latex]\text{X}[/latex] to point [latex]\text{Y}[/latex], as shown in the picture below. To find the length of the footbridge, she draws a right triangle [latex]\text{XYZ}[/latex], with right angle at [latex]\text{X}[/latex]. She measures the distance from [latex]\text{X}[/latex] to [latex]\text{Z},800[/latex] feet, and from [latex]\text{Y}[/latex] to [latex]\text{Z},1,000[/latex] feet. How long will the bridge be?

Writing Exercises

Write three of the properties of triangles from this section and then explain each in your own words.

Answers will vary.

Explain how the figure below illustrates the Pythagorean Theorem for a triangle with legs of length [latex]3[/latex] and [latex]4[/latex].

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?

Use Properties of Angles, Triangles, and the Pythagorean Theorem

Use Properties of Angles
In the following exercises, solve using properties of angles.

What is the supplement of a [latex]{48^\circ }[/latex] angle?

132°

What is the complement of a [latex]{61^\circ }[/latex] angle?

Two angles are complementary. The smaller angle is [latex]{24^\circ }[/latex] less than the larger angle. Find the measures of both angles.

33°, 57°

Two angles are supplementary. The larger angle is [latex]{45^\circ }[/latex] more than the smaller angle. Find the measures of both angles.

Use Properties of Triangles
In the following exercises, solve using properties of triangles.

The measures of two angles of a triangle are [latex]22[/latex] and [latex]85[/latex] degrees. Find the measure of the third angle.

73°

One angle of a right triangle measures [latex]41.5[/latex] degrees. What is the measure of the other small angle?

One angle of a triangle is [latex]{30^\circ }[/latex] more than the smallest angle. The largest angle is the sum of the other angles. Find the measures of all three angles.

30°, 60°, 90°

One angle of a triangle is twice the measure of the smallest angle. The third angle is [latex]{60^\circ }[/latex] more than the measure of the smallest angle. Find the measures of all three angles.

In the following exercises, [latex]\Delta ABC[/latex] is similar to [latex]\Delta XYZ[/latex]. Find the length of the indicated side.

side [latex]x[/latex]

15

side [latex]b[/latex]

Use the Pythagorean Theorem
In the following exercises, use the Pythagorean Theorem to find the length of the missing side. Round to the nearest tenth, if necessary.

26

8

8.1

In the following exercises, solve. Approximate to the nearest tenth, if necessary.

Sergio needs to attach a wire to hold the antenna to the roof of his house, as shown in the figure. The antenna is [latex]8[/latex] feet tall and Sergio has [latex]10[/latex] feet of wire. How far from the base of the antenna can he attach the wire?

6 feet

Seong is building shelving in his garage. The shelves are [latex]36[/latex] inches wide and [latex]15[/latex] inches tall. He wants to put a diagonal brace across the back to stabilize the shelves, as shown. How long should the brace be?

Use Properties of Rectangles, Triangles, and Trapezoids

Understand Linear, Square, Cubic Measure
In the following exercises, would you measure each item using linear, square, or cubic measure?

amount of sand in a sandbag

cubic

height of a tree

size of a patio

square

length of a highway

In the following exercises, find

ⓐ the perimeter
ⓑ the area of each figure

ⓐ 8 units
ⓑ 3 sq. units

Use Properties of Rectangles In the following exercises, find the

ⓐ perimeter
ⓑ area of each rectangle

The length of a rectangle is [latex]42[/latex] meters and the width is [latex]28[/latex] meters.

ⓐ 140 m
ⓑ 1176 sq. m

The length of a rectangle is [latex]36[/latex] feet and the width is [latex]19[/latex] feet.

A sidewalk in front of Kathy’s house is in the shape of a rectangle [latex]4[/latex] feet wide by [latex]45[/latex] feet long.

ⓐ 98 ft.
ⓑ 180 sq. ft.

A rectangular room is [latex]16[/latex] feet wide by [latex]12[/latex] feet long.

In the following exercises, solve.

Find the length of a rectangle with perimeter of [latex]220[/latex] centimeters and width of [latex]85[/latex] centimeters.

25 cm

Find the width of a rectangle with perimeter [latex]39[/latex] and length [latex]11[/latex].

The area of a rectangle is [latex]2356[/latex] square meters. The length is [latex]38[/latex] meters. What is the width?

62 m

The width of a rectangle is [latex]45[/latex] centimeters. The area is [latex]2700[/latex] square centimeters. What is the length?

The length of a rectangle is [latex]12[/latex] centimeters more than the width. The perimeter is [latex]74[/latex] centimeters. Find the length and the width.

24.5 in., 12.5 in.

The width of a rectangle is [latex]3[/latex] more than twice the length. The perimeter is [latex]96[/latex] inches. Find the length and the width.

Use Properties of Triangles
In the following exercises, solve using the properties of triangles.

Find the area of a triangle with base [latex]18[/latex] inches and height [latex]15[/latex] inches.

135 sq. in.

Find the area of a triangle with base [latex]33[/latex] centimeters and height [latex]21[/latex] centimeters.

A triangular road sign has base [latex]30[/latex] inches and height [latex]40[/latex] inches. What is its area?

600 sq. in.

If a triangular courtyard has sides [latex]9[/latex] feet and [latex]12[/latex] feet and the perimeter is [latex]32[/latex] feet, how long is the third side?

A tile in the shape of an isosceles triangle has a base of [latex]6[/latex] inches. If the perimeter is [latex]20[/latex] inches, find the length of each of the other sides.

7 in., 7 in.

Find the length of each side of an equilateral triangle with perimeter of [latex]81[/latex] yards.

The perimeter of a triangle is [latex]59[/latex] feet. One side of the triangle is [latex]3[/latex] feet longer than the shortest side. The third side is [latex]5[/latex] feet longer than the shortest side. Find the length of each side.

17 ft., 20 ft., 22 ft.

One side of a triangle is three times the smallest side. The third side is [latex]9[/latex] feet more than the shortest side. The perimeter is [latex]39[/latex] feet. Find the lengths of all three sides.

Use Properties of Trapezoids
In the following exercises, solve using the properties of trapezoids.

The height of a trapezoid is [latex]8[/latex] feet and the bases are [latex]11[/latex] and [latex]14[/latex] feet. What is the area?

100 sq. ft.

The height of a trapezoid is [latex]5[/latex] yards and the bases are [latex]7[/latex] and [latex]10[/latex] yards. What is the area?

Find the area of the trapezoid with height [latex]25[/latex] meters and bases [latex]32.5[/latex] and [latex]21.5[/latex] meters.

675 sq. m

A flag is shaped like a trapezoid with height [latex]62[/latex] centimeters and the bases are [latex]91.5[/latex] and [latex]78.1[/latex] centimeters. What is the area of the flag?

Practice Makes Perfect

Understand Linear, Square, and Cubic Measure
In the following exercises, determine whether you would measure each item using linear, square, or cubic units.

amount of water in a fish tank

cubic

length of dental floss

living area of an apartment

square

floor space of a bathroom tile

height of a doorway

linear

capacity of a truck trailer

In the following exercises, find the ⓐ perimeter and ⓑ area of each figure. Assume each side of the square is [latex]1[/latex] cm.

ⓐ 10 cm
ⓑ 4 sq. cm

ⓐ 8 cm
ⓑ 3 sq. cm

ⓐ 10 cm
ⓑ 5 sq. cm

Use the Properties of Rectangles
In the following exercises, find the ⓐ perimeter and ⓑ area of each rectangle.

The length of a rectangle is [latex]85[/latex] feet and the width is [latex]45[/latex] feet.

ⓐ 260 ft
ⓑ 3825 sq. ft

The length of a rectangle is [latex]26[/latex] inches and the width is [latex]58[/latex] inches.

A rectangular room is [latex]15[/latex] feet wide by [latex]14[/latex] feet long.

ⓐ 58 ft
ⓑ 210 sq. ft

A driveway is in the shape of a rectangle [latex]20[/latex] feet wide by [latex]35[/latex] feet long.

In the following exercises, solve.

Find the length of a rectangle with perimeter [latex]124[/latex] inches and width [latex]38[/latex] inches.

24 inches

Find the length of a rectangle with perimeter [latex]20.2[/latex] yards and width of [latex]7.8[/latex] yards.

Find the width of a rectangle with perimeter [latex]92[/latex] meters and length [latex]19[/latex] meters.

27 meters

Find the width of a rectangle with perimeter [latex]16.2[/latex] meters and length [latex]3.2[/latex] meters.

The area of a rectangle is [latex]414[/latex] square meters. The length is [latex]18[/latex] meters. What is the width?

23 m

The area of a rectangle is [latex]782[/latex] square centimeters. The width is [latex]17[/latex] centimeters. What is the length?

The length of a rectangle is [latex]9[/latex] inches more than the width. The perimeter is [latex]46[/latex] inches. Find the length and the width.

7 in., 16 in.

The width of a rectangle is [latex]8[/latex] inches more than the length. The perimeter is [latex]52[/latex] inches. Find the length and the width.

The perimeter of a rectangle is [latex]58[/latex] meters. The width of the rectangle is [latex]5[/latex] meters less than the length. Find the length and the width of the rectangle.

17 m, 12 m

The perimeter of a rectangle is [latex]62[/latex] feet. The width is [latex]7[/latex] feet less than the length. Find the length and the width.

The width of the rectangle is [latex]0.7[/latex] meters less than the length. The perimeter of a rectangle is [latex]52.6[/latex] meters. Find the dimensions of the rectangle.

13.5 m, 12.8 m

The length of the rectangle is [latex]1.1[/latex] meters less than the width. The perimeter of a rectangle is [latex]49.4[/latex] meters. Find the dimensions of the rectangle.

The perimeter of a rectangle of [latex]150[/latex] feet. The length of the rectangle is twice the width. Find the length and width of the rectangle.

25 ft, 50 ft

The length of a rectangle is three times the width. The perimeter is [latex]72[/latex] feet. Find the length and width of the rectangle.

The length of a rectangle is [latex]3[/latex] meters less than twice the width. The perimeter is [latex]36[/latex] meters. Find the length and width.

7 m, 11 m

The length of a rectangle is [latex]5[/latex] inches more than twice the width. The perimeter is [latex]34[/latex] inches. Find the length and width.

The width of a rectangular window is [latex]24[/latex] inches. The area is [latex]624[/latex] square inches. What is the length?

26 in.

The length of a rectangular poster is [latex]28[/latex] inches. The area is [latex]1316[/latex] square inches. What is the width?

The area of a rectangular roof is [latex]2310[/latex] square meters. The length is [latex]42[/latex] meters. What is the width?

55 m

The area of a rectangular tarp is [latex]132[/latex] square feet. The width is [latex]12[/latex] feet. What is the length?

The perimeter of a rectangular courtyard is [latex]160[/latex] feet. The length is [latex]10[/latex] feet more than the width. Find the length and the width.

35 ft, 45 ft

The perimeter of a rectangular painting is [latex]306[/latex] centimeters. The length is [latex]17[/latex] centimeters more than the width. Find the length and the width.

The width of a rectangular window is [latex]40[/latex] inches less than the height. The perimeter of the doorway is [latex]224[/latex] inches. Find the length and the width.

76 in., 36 in.

The width of a rectangular playground is [latex]7[/latex] meters less than the length. The perimeter of the playground is [latex]46[/latex] meters. Find the length and the width.

Use the Properties of Triangles
In the following exercises, solve using the properties of triangles.

Find the area of a triangle with base [latex]12[/latex] inches and height [latex]5[/latex] inches.

60 sq. in.

Find the area of a triangle with base [latex]45[/latex] centimeters and height [latex]30[/latex] centimeters.

Find the area of a triangle with base [latex]8.3[/latex] meters and height [latex]6.1[/latex] meters.

25.315 sq. m

Find the area of a triangle with base [latex]24.2[/latex] feet and height [latex]20.5[/latex] feet.

A triangular flag has base of [latex]1[/latex] foot and height of [latex]1.5[/latex] feet. What is its area?

0.75 sq. ft

A triangular window has base of [latex]8[/latex] feet and height of [latex]6[/latex] feet. What is its area?

If a triangle has sides of [latex]6[/latex] feet and [latex]9[/latex] feet and the perimeter is [latex]23[/latex] feet, how long is the third side?

8 ft

If a triangle has sides of [latex]14[/latex] centimeters and [latex]18[/latex] centimeters and the perimeter is [latex]49[/latex] centimeters, how long is the third side?

What is the base of a triangle with an area of [latex]207[/latex] square inches and height of [latex]18[/latex] inches?

23 in.

What is the height of a triangle with an area of [latex]893[/latex] square inches and base of [latex]38[/latex] inches?

The perimeter of a triangular reflecting pool is [latex]36[/latex] yards. The lengths of two sides are [latex]10[/latex] yards and [latex]15[/latex] yards. How long is the third side?

11 ft

A triangular courtyard has perimeter of [latex]120[/latex] meters. The lengths of two sides are [latex]30[/latex] meters and [latex]50[/latex] meters. How long is the third side?

An isosceles triangle has a base of [latex]20[/latex] centimeters. If the perimeter is [latex]76[/latex] centimeters, find the length of each of the other sides.

28 cm

An isosceles triangle has a base of [latex]25[/latex] inches. If the perimeter is [latex]95[/latex] inches, find the length of each of the other sides.

Find the length of each side of an equilateral triangle with a perimeter of [latex]51[/latex] yards.

17 ft

Find the length of each side of an equilateral triangle with a perimeter of [latex]54[/latex] meters.

The perimeter of an equilateral triangle is [latex]18[/latex] meters. Find the length of each side.

6 m

The perimeter of an equilateral triangle is [latex]42[/latex] miles. Find the length of each side.

The perimeter of an isosceles triangle is [latex]42[/latex] feet. The length of the shortest side is [latex]12[/latex] feet. Find the length of the other two sides.

15 ft

The perimeter of an isosceles triangle is [latex]83[/latex] inches. The length of the shortest side is [latex]24[/latex] inches. Find the length of the other two sides.

A dish is in the shape of an equilateral triangle. Each side is [latex]8[/latex] inches long. Find the perimeter.

24 in.

A floor tile is in the shape of an equilateral triangle. Each side is [latex]1.5[/latex] feet long. Find the perimeter.

A road sign in the shape of an isosceles triangle has a base of [latex]36[/latex] inches. If the perimeter is [latex]91[/latex] inches, find the length of each of the other sides.

27.5 in.

A scarf in the shape of an isosceles triangle has a base of [latex]0.75[/latex] meters. If the perimeter is [latex]2[/latex] meters, find the length of each of the other sides.

The perimeter of a triangle is [latex]39[/latex] feet. One side of the triangle is [latex]1[/latex] foot longer than the second side. The third side is [latex]2[/latex] feet longer than the second side. Find the length of each side.

12 ft, 13 ft, 14 ft

The perimeter of a triangle is [latex]35[/latex] feet. One side of the triangle is [latex]5[/latex] feet longer than the second side. The third side is [latex]3[/latex] feet longer than the second side. Find the length of each side.

One side of a triangle is twice the smallest side. The third side is [latex]5[/latex] feet more than the shortest side. The perimeter is [latex]17[/latex] feet. Find the lengths of all three sides.

3 ft, 6 ft, 8 ft

One side of a triangle is three times the smallest side. The third side is [latex]3[/latex] feet more than the shortest side. The perimeter is [latex]13[/latex] feet. Find the lengths of all three sides.

Use the Properties of Trapezoids
In the following exercises, solve using the properties of trapezoids.

The height of a trapezoid is [latex]12[/latex] feet and the bases are [latex]9[/latex] and [latex]15[/latex] feet. What is the area?

144 sq. ft

The height of a trapezoid is [latex]24[/latex] yards and the bases are [latex]18[/latex] and [latex]30[/latex] yards. What is the area?

Find the area of a trapezoid with a height of [latex]51[/latex] meters and bases of [latex]43[/latex] and [latex]67[/latex] meters.

2805 sq. m

Find the area of a trapezoid with a height of [latex]62[/latex] inches and bases of [latex]58[/latex] and [latex]75[/latex] inches.

The height of a trapezoid is [latex]15[/latex] centimeters and the bases are [latex]12.5[/latex] and [latex]18.3[/latex] centimeters. What is the area?

231 sq. cm

The height of a trapezoid is [latex]48[/latex] feet and the bases are [latex]38.6[/latex] and [latex]60.2[/latex] feet. What is the area?

Find the area of a trapezoid with a height of [latex]4.2[/latex] meters and bases of [latex]8.1[/latex] and [latex]5.5[/latex] meters.

28.56 sq. m

Find the area of a trapezoid with a height of [latex]32.5[/latex] centimeters and bases of [latex]54.6[/latex] and [latex]41.4[/latex] centimeters.

Laurel is making a banner shaped like a trapezoid. The height of the banner is [latex]3[/latex] feet and the bases are [latex]4[/latex] and [latex]5[/latex] feet. What is the area of the banner?

13.5 sq. ft

Niko wants to tile the floor of his bathroom. The floor is shaped like a trapezoid with width [latex]5[/latex] feet and lengths [latex]5[/latex] feet and [latex]8[/latex] feet. What is the area of the floor?

Theresa needs a new top for her kitchen counter. The counter is shaped like a trapezoid with width [latex]18.5[/latex] inches and lengths [latex]62[/latex] and [latex]50[/latex] inches. What is the area of the counter?

1036 sq. in.

Elena is knitting a scarf. The scarf will be shaped like a trapezoid with width [latex]8[/latex] inches and lengths [latex]48.2[/latex] inches and [latex]56.2[/latex] inches. What is the area of the scarf?

Everyday Math

Fence Jose just removed the children’s playset from his back yard to make room for a rectangular garden. He wants to put a fence around the garden to keep out the dog. He has a [latex]50[/latex] foot roll of fence in his garage that he plans to use. To fit in the backyard, the width of the garden must be [latex]10[/latex] feet. How long can he make the other side if he wants to use the entire roll of fence?

15 ft

Gardening Lupita wants to fence in her tomato garden. The garden is rectangular and the length is twice the width. It will take [latex]48[/latex] feet of fencing to enclose the garden. Find the length and width of her garden.

Fence Christa wants to put a fence around her triangular flowerbed. The sides of the flowerbed are [latex]6[/latex] feet, [latex]8[/latex] feet, and [latex]10[/latex] feet. The fence costs [latex]$10[/latex] per foot. How much will it cost for Christa to fence in her flowerbed?

$24

Painting Caleb wants to paint one wall of his attic. The wall is shaped like a trapezoid with height [latex]8[/latex] feet and bases [latex]20[/latex] feet and [latex]12[/latex] feet. The cost of the painting one square foot of wall is about [latex]$0.05[/latex]. About how much will it cost for Caleb to paint the attic wall?

Writing Exercises

If you need to put tile on your kitchen floor, do you need to know the perimeter or the area of the kitchen? Explain your reasoning.

Answers will vary.

If you need to put a fence around your backyard, do you need to know the perimeter or the area of the backyard? Explain your reasoning.

Look at the two figures.

ⓐ Which figure looks like it has the larger area? Which looks like it has the larger perimeter?
ⓑ Now calculate the area and perimeter of each figure. Which has the larger area? Which has the larger perimeter?

Answers will vary.

The length of a rectangle is [latex]5[/latex] feet more than the width. The area is [latex]50[/latex] square feet. Find the length and the width.
ⓐ Write the equation you would use to solve the problem.
ⓑ Why can’t you solve this equation with the methods you learned in the previous chapter?

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ On a scale of 1–10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?

Solve Geometry Applications: Circles and Irregular Figures

Use Properties of Circles
In the following exercises, solve using the properties of circles. Round answers to the nearest hundredth.

A circular mosaic has radius [latex]3[/latex] meters. Find the

ⓐ circumference
ⓑ area of the mosaic

ⓐ 18.84 m
ⓑ 28.26 sq. m

A circular fountain has radius [latex]8[/latex] feet. Find the

ⓐ circumference
ⓑ area of the fountain

Find the diameter of a circle with circumference [latex]150.72[/latex] inches.

48 in.

Find the radius of a circle with circumference [latex]345.4[/latex] centimeters

Find the Area of Irregular Figures
In the following exercises, find the area of each shaded region.

30 sq. units

300 sq. units

199.25 sq. units

Solve Geometry Applications: Volume and Surface Area

Find Volume and Surface Area of Rectangular Solids
In the following exercises, find the

ⓐ volume
ⓑ surface area of the rectangular solid

a rectangular solid with length [latex]14[/latex] centimeters, width [latex]4.5[/latex] centimeters, and height [latex]10[/latex] centimeters

ⓐ 630 cu. cm
ⓑ 496 sq. cm

a cube with sides that are [latex]3[/latex] feet long

a cube of tofu with sides [latex]2.5[/latex] inches

ⓐ 15.625 cu. in.
ⓑ 37.5 sq. in.

a rectangular carton with length [latex]32[/latex] inches, width [latex]18[/latex] inches, and height [latex]10[/latex] inches

Find Volume and Surface Area of Spheres
In the following exercises, find the

ⓐ volume
ⓑ surface area of the sphere.

a sphere with radius [latex]4[/latex] yards

ⓐ 267.95 cu. yd.
ⓑ 200.96 sq. yd.

a sphere with radius [latex]12[/latex] meters

a baseball with radius [latex]1.45[/latex] inches

ⓐ 12.76 cu. in.
ⓑ 26.41 sq. in.

a soccer ball with radius [latex]22[/latex] centimeters

Find Volume and Surface Area of Cylinders
In the following exercises, find the

ⓐ volume
ⓑ surface area of the cylinder

a cylinder with radius [latex]2[/latex] yards and height [latex]6[/latex] yards

ⓐ 75.36 cu. yd.
ⓑ 100.48 sq. yd.

a cylinder with diameter [latex]18[/latex] inches and height [latex]40[/latex] inches

a juice can with diameter [latex]8[/latex] centimeters and height [latex]15[/latex] centimeters

ⓐ 753.6 cu. cm
ⓑ 477.28 sq. cm

a cylindrical pylon with diameter [latex]0.8[/latex] feet and height [latex]2.5[/latex] feet

Find Volume of Cones
In the following exercises, find the volume of the cone.

a cone with height [latex]5[/latex] meters and radius [latex]1[/latex] meter

5.233 cu. m

a cone with height [latex]24[/latex] feet and radius [latex]8[/latex] feet

a cone-shaped water cup with diameter [latex]2.6[/latex] inches and height [latex]2.6[/latex] inches

4.599 cu. in.

a cone-shaped pile of gravel with diameter [latex]6[/latex] yards and height [latex]5[/latex] yards

Find the complement of a [latex]{52^\circ }[/latex] angle.

38°

The measure of one angle of a triangle is twice the measure of the smallest angle. The measure of the third angle is [latex]14[/latex] more than the measure of the smallest angle. Find the measures of all three angles.

The perimeter of an equilateral triangle is [latex]145[/latex] feet. Find the length of each side.

48.3

[latex]\Delta ABC[/latex] is similar to [latex]\Delta XYZ[/latex]. Find the length of side [latex]c[/latex].

Find the length of the missing side. Round to the nearest tenth, if necessary.

10

Find the length of the missing side. Round to the nearest tenth, if necessary.

A baseball diamond is shaped like a square with sides [latex]90[/latex] feet long. How far is it from home plate to second base, as shown?

127.3 ft

The length of a rectangle is [latex]2[/latex] feet more than five times the width. The perimeter is [latex]40[/latex] feet. Find the dimensions of the rectangle.

A triangular poster has base [latex]80[/latex] centimeters and height [latex]55[/latex] centimeters. Find the area of the poster.

2200 square centimeters

A trapezoid has height [latex]14[/latex] inches and bases [latex]20[/latex] inches and [latex]23[/latex] inches. Find the area of the trapezoid.

A circular pool has diameter [latex]90[/latex] inches. What is its circumference? Round to the nearest tenth.

282.6 inches

Find the area of the shaded region. Round to the nearest tenth.

Find the volume of a rectangular room with width [latex]12[/latex] feet, length [latex]15[/latex] feet, and height [latex]8[/latex] feet.

1440

A coffee can is shaped like a cylinder with height [latex]7[/latex] inches and radius [latex]5[/latex] inches. Find (a) the surface area and (b) the volume of the can. Round to the nearest tenth.

A traffic cone has height [latex]75[/latex] centimeters. The radius of the base is [latex]20[/latex] centimeters. Find the volume of the cone. Round to the nearest tenth.

31,400 cubic inches

Solve the formula [latex]A=\Large\frac{1}{2}\normalsize bh[/latex] for [latex]h\text{:}[/latex]

ⓐ when [latex]A=1716[/latex] and [latex]b=66[/latex]
ⓑ in general

ⓐ [latex]\text{height}=52[/latex]
ⓑ [latex]h=\Large\frac{2A}{b}[/latex]

Solve [latex]x+5y=14[/latex] for [latex]y[/latex].

Practice Makes Perfect

Use the Properties of Circles
In the following exercises, solve using the properties of circles.

The lid of a paint bucket is a circle with radius [latex]7[/latex] inches. Find the ⓐ circumference and ⓑ area of the lid.

ⓐ 43.96 in.
ⓑ 153.86 sq. in.

An extra-large pizza is a circle with radius [latex]8[/latex] inches. Find the ⓐ circumference and ⓑ area of the pizza.

A farm sprinkler spreads water in a circle with radius of [latex]8.5[/latex] feet. Find the ⓐ circumference and ⓑ area of the watered circle.

ⓐ 53.38 ft
ⓑ 226.865 sq. ft

A circular rug has radius of [latex]3.5[/latex] feet. Find the ⓐ circumference and ⓑ area of the rug.

A reflecting pool is in the shape of a circle with diameter of [latex]20[/latex] feet. What is the circumference of the pool?

62.8 ft

A turntable is a circle with diameter of [latex]10[/latex] inches. What is the circumference of the turntable?

A circular saw has a diameter of [latex]12[/latex] inches. What is the circumference of the saw?

37.68 in.

A round coin has a diameter of [latex]3[/latex] centimeters. What is the circumference of the coin?

A barbecue grill is a circle with a diameter of [latex]2.2[/latex] feet. What is the circumference of the grill?

6.908 ft

The top of a pie tin is a circle with a diameter of [latex]9.5[/latex] inches. What is the circumference of the top?

A circle has a circumference of [latex]163.28[/latex] inches. Find the diameter.

52 in.

A circle has a circumference of [latex]59.66[/latex] feet. Find the diameter.

A circle has a circumference of [latex]17.27[/latex] meters. Find the diameter.

5.5 m

A circle has a circumference of [latex]80.07[/latex] centimeters. Find the diameter.

In the following exercises, find the radius of the circle with given circumference.

A circle has a circumference of [latex]150.72[/latex] feet.

24 ft

A circle has a circumference of [latex]251.2[/latex] centimeters.

A circle has a circumference of [latex]40.82[/latex] miles.

6.5 mi

A circle has a circumference of [latex]78.5[/latex] inches.

Find the Area of Irregular Figures
In the following exercises, find the area of the irregular figure. Round your answers to the nearest hundredth.

16 sq. units

30 sq. units

57.5 sq. units

12 sq. units

67.5 sq. units

89 sq. units

44.81 sq. units

41.12 sq. units

35.13 sq. units

95.625 sq. units

In the following exercises, solve.

A city park covers one block plus parts of four more blocks, as shown. The block is a square with sides [latex]250[/latex] feet long, and the triangles are isosceles right triangles. Find the area of the park.

187,500 sq. ft

A gift box will be made from a rectangular piece of cardboard measuring [latex]12[/latex] inches by [latex]20[/latex] inches, with squares cut out of the corners of the sides, as shown. The sides of the squares are [latex]3[/latex] inches. Find the area of the cardboard after the corners are cut out.

Perry needs to put in a new lawn. His lot is a rectangle with a length of [latex]120[/latex] feet and a width of [latex]100[/latex] feet. The house is rectangular and measures [latex]50[/latex] feet by [latex]40[/latex] feet. His driveway is rectangular and measures [latex]20[/latex] feet by [latex]30[/latex] feet, as shown. Find the area of Perry’s lawn.

9400 sq. ft

Denise is planning to put a deck in her back yard. The deck will be a [latex]\text{20-ft}[/latex] by [latex]\text{12-ft}[/latex] rectangle with a semicircle of diameter [latex]6[/latex] feet, as shown below. Find the area of the deck.

Everyday Math

Area of a Tabletop Yuki bought a drop-leaf kitchen table. The rectangular part of the table is a [latex]\text{1-ft}[/latex] by [latex]\text{3-ft}[/latex] rectangle with a semicircle at each end, as shown. ⓐ Find the area of the table with one leaf up. ⓑ Find the area of the table with both leaves up.

ⓐ 6.5325 sq. ft
ⓑ 10.065 sq. ft

Painting Leora wants to paint the nursery in her house. The nursery is an [latex]\text{8-ft}[/latex] by [latex]\text{10-ft}[/latex] rectangle, and the ceiling is [latex]8[/latex] feet tall. There is a [latex]\text{3-ft}[/latex] by [latex]\text{6.5-ft}[/latex] door on one wall, a [latex]\text{3-ft}[/latex] by [latex]\text{6.5-ft}[/latex] closet door on another wall, and one [latex]\text{4-ft}[/latex] by [latex]\text{3.5-ft}[/latex] window on the third wall. The fourth wall has no doors or windows. If she will only paint the four walls, and not the ceiling or doors, how many square feet will she need to paint?

Writing Exercises

Describe two different ways to find the area of this figure, and then show your work to make sure both ways give the same area.

Answers will vary.

A circle has a diameter of [latex]14[/latex] feet. Find the area of the circle ⓐ using [latex]3.14[/latex] for [latex]\pi [/latex] ⓑ using [latex]\Large\frac{22}{7}[/latex] for [latex]\text{\pi }[/latex]. ⓒ Which calculation to do prefer? Why?

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After looking at the checklist, do you think you are well prepared for the next section? Why or why not?

Practice Makes Perfect

Find Volume and Surface Area of Rectangular Solids
In the following exercises, find ⓐ the volume and ⓑ the surface area of the rectangular solid with the given dimensions.

length [latex]2[/latex] meters, width [latex]1.5[/latex] meters, height [latex]3[/latex] meters

ⓐ 9 cu. m
ⓑ 27 sq. m

length [latex]5[/latex] feet, width [latex]8[/latex] feet, height [latex]2.5[/latex] feet

length [latex]3.5[/latex] yards, width [latex]2.1[/latex] yards, height [latex]2.4[/latex] yards

ⓐ 17.64 cu. yd.
ⓑ 41.58 sq. yd.

length [latex]8.8[/latex] centimeters, width [latex]6.5[/latex] centimeters, height [latex]4.2[/latex] centimeters

In the following exercises, solve.

Moving van A rectangular moving van has length [latex]16[/latex] feet, width [latex]8[/latex] feet, and height [latex]8[/latex] feet. Find its ⓐ volume and ⓑ surface area.

ⓐ 1,024 cu. ft
ⓑ 640 sq. ft

Gift box A rectangular gift box has length [latex]26[/latex] inches, width [latex]16[/latex] inches, and height
[latex]4[/latex] inches. Find its ⓐ volume and ⓑ surface area.

Carton A rectangular carton has length
[latex]21.3[/latex] cm, width [latex]24.2[/latex] cm, and height [latex]6.5[/latex] cm. Find its ⓐ volume and ⓑ surface area.

ⓐ 3,350.49 cu. cm
ⓑ 1,622.42 sq. cm

Shipping container A rectangular shipping container has length [latex]22.8[/latex] feet, width [latex]8.5[/latex] feet, and height [latex]8.2[/latex] feet. Find its ⓐ volume and ⓑ surface area.

In the following exercises, find ⓐ the volume and ⓑ the surface area of the cube with the given side length.

[latex]5[/latex] centimeters

ⓐ 125 cu. cm
ⓑ 150 sq. cm

[latex]6[/latex] inches

[latex]10.4[/latex] feet

ⓐ 1124.864 cu. ft.
ⓑ 648.96 sq. ft

[latex]12.5[/latex] meters

In the following exercises, solve.

Science center Each side of the cube at the Discovery Science Center in Santa Ana is [latex]64[/latex] feet long. Find its ⓐ volume and ⓑ surface area.

ⓐ 262,144 cu. ft
ⓑ 24,576 sq. ft

Museum A cube-shaped museum has sides [latex]45[/latex] meters long. Find its ⓐ volume and ⓑ surface area.

Base of statue The base of a statue is a cube with sides [latex]2.8[/latex] meters long. Find its ⓐ volume and ⓑ surface area.

ⓐ 21.952 cu. m
ⓑ 47.04 sq. m

Tissue box A box of tissues is a cube with sides 4.5 inches long. Find its ⓐ volume and ⓑ surface area.

Find the Volume and Surface Area of Spheres In the following exercises, find ⓐ the volume and ⓑ the surface area of the sphere with the given radius. Round answers to the nearest hundredth.

[latex]3[/latex] centimeters

ⓐ 113.04 cu. cm
ⓑ 113.04 sq. cm

[latex]9[/latex] inches

[latex]7.5[/latex] feet

ⓐ 1,766.25 cu. ft
ⓑ 706.5 sq. ft

[latex]2.1[/latex] yards

In the following exercises, solve. Round answers to the nearest hundredth.

Exercise ball An exercise ball has a radius of [latex]15[/latex] inches. Find its ⓐ volume and ⓑ surface area.

ⓐ 14,130 cu. in.
ⓑ 2,826 sq. in.

Balloon ride The Great Park Balloon is a big orange sphere with a radius of [latex]36[/latex] feet . Find its ⓐ volume and ⓑ surface area.

Golf ball A golf ball has a radius of [latex]4.5[/latex] centimeters. Find its ⓐ volume and ⓑ surface area.

ⓐ 381.51 cu. cm
ⓑ 254.34 sq. cm

Baseball A baseball has a radius of [latex]2.9[/latex] inches. Find its ⓐ volume and ⓑ surface area.

Find the Volume and Surface Area of a Cylinder
In the following exercises, find ⓐ the volume and ⓑ the surface area of the cylinder with the given radius and height. Round answers to the nearest hundredth.

radius [latex]3[/latex] feet, height [latex]9[/latex] feet

ⓐ 254.34 cu. ft
ⓑ 226.08 sq. ft

radius [latex]5[/latex] centimeters, height [latex]15[/latex] centimeters

radius [latex]1.5[/latex] meters, height [latex]4.2[/latex] meters

ⓐ 29.673 cu. m
ⓑ 53.694 sq. m

radius [latex]1.3[/latex] yards, height [latex]2.8[/latex] yards

In the following exercises, solve. Round answers to the nearest hundredth.

Coffee can A can of coffee has a radius of [latex]5[/latex] cm and a height of [latex]13[/latex] cm. Find its ⓐ volume and ⓑ surface area.

ⓐ 1,020.5 cu. cm
ⓑ 565.2 sq. cm

Snack pack A snack pack of cookies is shaped like a cylinder with radius [latex]4[/latex] cm and height [latex]3[/latex] cm. Find its ⓐ volume and ⓑ surface area.

Barber shop pole A cylindrical barber shop pole has a diameter of [latex]6[/latex] inches and height of [latex]24[/latex] inches. Find its ⓐ volume and ⓑ surface area.

ⓐ 678.24 cu. in.
ⓑ 508.68 sq. in.

Architecture A cylindrical column has a diameter of [latex]8[/latex] feet and a height of [latex]28[/latex] feet. Find its ⓐ volume and ⓑ surface area.

Find the Volume of Cones
In the following exercises, find the volume of the cone with the given dimensions. Round answers to the nearest hundredth.

height [latex]9[/latex] feet and radius [latex]2[/latex] feet

37.68 cu. ft

height [latex]8[/latex] inches and radius [latex]6[/latex] inches

height [latex]12.4[/latex] centimeters and radius [latex]5[/latex] cm

324.47 cu. cm

height [latex]15.2[/latex] meters and radius [latex]4[/latex] meters

In the following exercises, solve. Round answers to the nearest hundredth.

Teepee What is the volume of a cone-shaped teepee tent that is [latex]10[/latex] feet tall and [latex]10[/latex] feet across at the base?

261.67 cu. ft

Popcorn cup What is the volume of a cone-shaped popcorn cup that is [latex]8[/latex] inches tall and [latex]6[/latex] inches across at the base?

Silo What is the volume of a cone-shaped silo that is [latex]50[/latex] feet tall and [latex]70[/latex] feet across at the base?

64,108.33 cu. ft

Sand pile What is the volume of a cone-shaped pile of sand that is [latex]12[/latex] meters tall and [latex]30[/latex] meters across at the base?

Everyday Math

Street light post The post of a street light is shaped like a truncated cone, as shown in the picture below. It is a large cone minus a smaller top cone. The large cone is [latex]30[/latex] feet tall with base radius [latex]1[/latex] foot. The smaller cone is [latex]10[/latex] feet tall with base radius of [latex]0.5[/latex] feet. To the nearest tenth,
ⓐ find the volume of the large cone.
ⓑ find the volume of the small cone.
ⓒ find the volume of the post by subtracting the volume of the small cone from the volume of the large cone.

ⓐ 31.4 cu. ft
ⓑ 2.6 cu. ft
ⓒ 28.8 cu. ft

Ice cream cones A regular ice cream cone is 4 inches tall and has a diameter of [latex]2.5[/latex] inches. A waffle cone is [latex]7[/latex] inches tall and has a diameter of [latex]3.25[/latex] inches. To the nearest hundredth,
ⓐ find the volume of the regular ice cream cone.
ⓑ find the volume of the waffle cone.
ⓒ how much more ice cream fits in the waffle cone compared to the regular cone?

Writing Exercises

The formulas for the volume of a cylinder and a cone are similar. Explain how you can remember which formula goes with which shape.

Answers will vary.

Which has a larger volume, a cube of sides of [latex]8[/latex] feet or a sphere with a diameter of [latex]8[/latex] feet? Explain your reasoning.

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

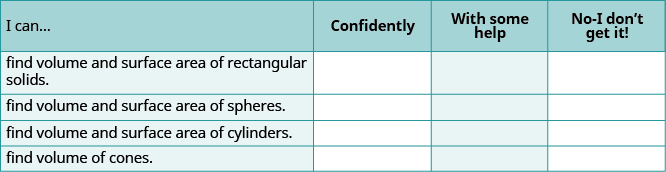
ⓑ After reviewing this checklist, what will you do to become confident for all objectives?

Practice Makes Perfect

Make Unit Conversions in the U.S. System
In the following exercises, convert the units.

A park bench is [latex]6[/latex] feet long. Convert the length to inches.

A floor tile is [latex]2[/latex] feet wide. Convert the width to inches.

24 inches

A ribbon is [latex]18[/latex] inches long. Convert the length to feet.

Carson is [latex]45[/latex] inches tall. Convert his height to feet.

3.75 feet

Jon is [latex]6[/latex] feet [latex]4[/latex] inches tall. Convert his height to inches.

Faye is [latex]4[/latex] feet [latex]10[/latex] inches tall. Convert her height to inches.

58 inches

A football field is [latex]160[/latex] feet wide. Convert the width to yards.

On a baseball diamond, the distance from home plate to first base is [latex]30[/latex] yards. Convert the distance to feet.

90 feet

Ulises lives [latex]1.5[/latex] miles from school. Convert the distance to feet.

Denver, Colorado, is [latex]5,183[/latex] feet above sea level. Convert the height to miles.

0.98 miles

A killer whale weighs [latex]4.6[/latex] tons. Convert the weight to pounds.

Blue whales can weigh as much as [latex]150[/latex] tons. Convert the weight to pounds.

300,000 pounds

An empty bus weighs [latex]35,000[/latex] pounds. Convert the weight to tons.

At take-off, an airplane weighs [latex]220,000[/latex] pounds. Convert the weight to tons.

110 tons

The voyage of the Mayflower took [latex]2[/latex] months and [latex]5[/latex] days. Convert the time to days.

Lynn’s cruise lasted [latex]6[/latex] days and [latex]18[/latex] hours. Convert the time to hours.

162 hours

Rocco waited [latex]1\Large\frac{1}{2}[/latex] hours for his appointment. Convert the time to seconds.

Misty’s surgery lasted [latex]2\Large\frac{1}{4}[/latex] hours. Convert the time to seconds.

8100 seconds

How many teaspoons are in a pint?

How many tablespoons are in a gallon?

256 tablespoons

JJ’s cat, Posy, weighs [latex]14[/latex] pounds. Convert her weight to ounces.

April’s dog, Beans, weighs [latex]8[/latex] pounds. Convert his weight to ounces.

128 ounces

Baby Preston weighed [latex]7[/latex] pounds [latex]3[/latex] ounces at birth. Convert his weight to ounces.

Baby Audrey weighed [latex]6[/latex] pounds [latex]15[/latex] ounces at birth. Convert her weight to ounces.

111 ounces

Crista will serve [latex]20[/latex] cups of juice at her son’s party. Convert the volume to gallons.

Lance needs [latex]500[/latex] cups of water for the runners in a race. Convert the volume to gallons.

31.25 gallons

Use Mixed Units of Measurement in the U.S. System
In the following exercises, solve and write your answer in mixed units.

Eli caught three fish. The weights of the fish were [latex]2[/latex] pounds [latex]4[/latex] ounces, [latex]1[/latex] pound [latex]11[/latex] ounces, and [latex]4[/latex] pounds [latex]14[/latex] ounces. What was the total weight of the three fish?

Judy bought [latex]1[/latex] pound [latex]6[/latex] ounces of almonds, [latex]2[/latex] pounds [latex]3[/latex] ounces of walnuts, and [latex]8[/latex] ounces of cashews. What was the total weight of the nuts?

4 lbs. 1 oz.

One day Anya kept track of the number of minutes she spent driving. She recorded trips of [latex]45,10,8,65,20,\text{and 35 minutes.}[/latex] How much time (in hours and minutes) did Anya spend driving?

Last year Eric went on [latex]6[/latex] business trips. The number of days of each was [latex]5,2,8,12,6,\text{and 3.}[/latex] How much time (in weeks and days) did Eric spend on business trips last year?

5 weeks and 1 day

Renee attached a [latex]\text{6-foot - 6-inch}[/latex] extension cord to her computer’s [latex]\text{3-foot - 8-inch}[/latex] power cord. What was the total length of the cords?

Fawzi’s SUV is [latex]6[/latex] feet [latex]4[/latex] inches tall. If he puts a [latex]\text{2-foot - 10-inch}[/latex] box on top of his SUV, what is the total height of the SUV and the box?

9 ft 2 in

Leilani wants to make [latex]8[/latex] placemats. For each placemat she needs [latex]18[/latex] inches of fabric. How many yards of fabric will she need for the [latex]8[/latex] placemats?

Mireille needs to cut [latex]24[/latex] inches of ribbon for each of the [latex]12[/latex] girls in her dance class. How many yards of ribbon will she need altogether?

8 yards

Make Unit Conversions in the Metric System
In the following exercises, convert the units.

Ghalib ran [latex]5[/latex] kilometers. Convert the length to meters.

Kitaka hiked [latex]8[/latex] kilometers. Convert the length to meters.

8000 meters

Estrella is [latex]1.55[/latex] meters tall. Convert her height to centimeters.

The width of the wading pool is [latex]2.45[/latex] meters. Convert the width to centimeters.

245 centimeters

Mount Whitney is [latex]3,072[/latex] meters tall. Convert the height to kilometers.

The depth of the Mariana Trench is [latex]10,911[/latex] meters. Convert the depth to kilometers.

10.911 kilometers

June’s multivitamin contains [latex]1,500[/latex] milligrams of calcium. Convert this to grams.

A typical ruby-throated hummingbird weights [latex]3[/latex] grams. Convert this to milligrams.

3000 milligrams

One stick of butter contains [latex]91.6[/latex] grams of fat. Convert this to milligrams.

One serving of gourmet ice cream has [latex]25[/latex] grams of fat. Convert this to milligrams.

25,000 milligrams

The maximum mass of an airmail letter is [latex]2[/latex] kilograms. Convert this to grams.

Dimitri’s daughter weighed [latex]3.8[/latex] kilograms at birth. Convert this to grams.

3800 grams

A bottle of wine contained [latex]750[/latex] milliliters. Convert this to liters.

A bottle of medicine contained [latex]300[/latex] milliliters. Convert this to liters.

0.3 liters

Use Mixed Units of Measurement in the Metric System
In the following exercises, solve and write your answer in mixed units.

Matthias is [latex]1.8[/latex] meters tall. His son is [latex]89[/latex] centimeters tall. How much taller, in centimeters, is Matthias than his son?

Stavros is [latex]1.6[/latex] meters tall. His sister is [latex]95[/latex] centimeters tall. How much taller, in centimeters, is Stavros than his sister?

65 centimeters

A typical dove weighs [latex]345[/latex] grams. A typical duck weighs [latex]1.2[/latex] kilograms. What is the difference, in grams, of the weights of a duck and a dove?

Concetta had a [latex]\text{2-kilogram}[/latex] bag of flour. She used [latex]180[/latex] grams of flour to make biscotti. How many kilograms of flour are left in the bag?

1.82 kilograms

Harry mailed [latex]5[/latex] packages that weighed [latex]420[/latex] grams each. What was the total weight of the packages in kilograms?

One glass of orange juice provides [latex]560[/latex] milligrams of potassium. Linda drinks one glass of orange juice every morning. How many grams of potassium does Linda get from her orange juice in [latex]30[/latex] days?

16.8 grams

Jonas drinks [latex]200[/latex] milliliters of water [latex]8[/latex] times a day. How many liters of water does Jonas drink in a day?

One serving of whole grain sandwich bread provides [latex]6[/latex] grams of protein. How many milligrams of protein are provided by [latex]7[/latex] servings of whole grain sandwich bread?

42,000 milligrams

Convert Between U.S. and Metric Systems
In the following exercises, make the unit conversions. Round to the nearest tenth.

Bill is [latex]75[/latex] inches tall. Convert his height to centimeters.

Frankie is [latex]42[/latex] inches tall. Convert his height to centimeters.

106.7 centimeters

Marcus passed a football [latex]24[/latex] yards. Convert the pass length to meters.

Connie bought [latex]9[/latex] yards of fabric to make drapes. Convert the fabric length to meters.

8.2 meters

Each American throws out an average of [latex]1,650[/latex] pounds of garbage per year. Convert this weight to kilograms.

An average American will throw away [latex]90,000[/latex] pounds of trash over his or her lifetime. Convert this weight to kilograms.

41,500 kilograms

A [latex]\text{5K}[/latex] run is [latex]5[/latex] kilometers long. Convert this length to miles.

Kathryn is [latex]1.6[/latex] meters tall. Convert her height to feet.

5.2 feet

Dawn’s suitcase weighed [latex]20[/latex] kilograms. Convert the weight to pounds.

Jackson’s backpack weighs [latex]15[/latex] kilograms. Convert the weight to pounds.

33 pounds

Ozzie put [latex]14[/latex] gallons of gas in his truck. Convert the volume to liters.

Bernard bought [latex]8[/latex] gallons of paint. Convert the volume to liters.

30.4 liters

Convert between Fahrenheit and Celsius
In the following exercises, convert the Fahrenheit temperature to degrees Celsius. Round to the nearest tenth.

[latex]86{^\circ F}[/latex]

[latex]77{^\circ F}[/latex]

25°C

[latex]104{^\circ F}[/latex]

[latex]14{^\circ F}[/latex]

−10°C

[latex]72{^\circ F}[/latex]

[latex]4{^\circ F}[/latex]

−15.5°C

[latex]0{^\circ F}[/latex]

[latex]120{^\circ F}[/latex]

48.9°C

In the following exercises, convert the Celsius temperatures to degrees Fahrenheit. Round to the nearest tenth.

[latex]5{^\circ C}[/latex]

[latex]25{^\circ C}[/latex]

77°F

[latex]-10{^\circ C}[/latex]

[latex]-15{^\circ C}[/latex]

5°F

[latex]22{^\circ C}[/latex]

[latex]8{^\circ C}[/latex]

46.4°F

[latex]43{^\circ C}[/latex]

[latex]16{^\circ C}[/latex]

60.8°F

Everyday Math

Nutrition Julian drinks one can of soda every day. Each can of soda contains [latex]40[/latex] grams of sugar. How many kilograms of sugar does Julian get from soda in [latex]1[/latex] year?

Reflectors The reflectors in each lane-marking stripe on a highway are spaced [latex]16[/latex] yards apart. How many reflectors are needed for a one-mile-long stretch of highway?

110 reflectors

Writing Exercises

Some people think that [latex]65{^\circ }[/latex] to [latex]75{^\circ }[/latex] Fahrenheit is the ideal temperature range.
ⓐ What is your ideal temperature range? Why do you think so?
ⓑ Convert your ideal temperatures from Fahrenheit to Celsius.

ⓐ Did you grow up using the U.S. customary or the metric system of measurement? ⓑ Describe two examples in your life when you had to convert between systems of measurement. ⓒ Which system do you think is easier to use? Explain.

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

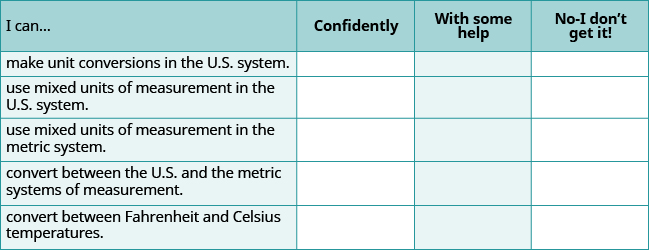
ⓑ Overall, after looking at the checklist, do you think you are well-prepared for the next chapter? Why or why not?

Chapter Review Exercises

Rational and Irrational Numbers

In the following exercises, write as the ratio of two integers.

[latex]6[/latex]

[latex]-5[/latex]

[latex]\Large\frac{-5}{1}[/latex]

[latex]2.9[/latex]

[latex]1.8[/latex]

[latex]\Large\frac{18}{10}[/latex]

In the following exercises, determine which of the numbers is rational.

[latex]0.42,0.\stackrel{\text{-}}{\text{3}},2.56813\dots [/latex]

[latex]{0.75319\ldots },0.\stackrel{\text{-}}{16},1.95[/latex]

[latex]0.\stackrel{\text{-}}{16},1.95[/latex]

In the following exercises, identify whether each given number is rational or irrational.

ⓐ [latex]\sqrt{49}[/latex] ⓑ [latex]\sqrt{55}[/latex]

ⓐ [latex]\sqrt{72}[/latex] ⓑ [latex]\sqrt{64}[/latex]

ⓐ irrational
ⓑ rational

In the following exercises, list the ⓐ whole numbers, ⓑ integers, ⓒ rational numbers, ⓓ irrational numbers, ⓔ real numbers for each set of numbers.

[latex]-9,0,\text{0.361….},\Large\frac{8}{9}\normalsize ,\sqrt{16},9[/latex]

[latex]-5,-2\Large\frac{1}{4}\normalsize ,-\sqrt{4},0.\stackrel{\text{-}}{25},\Large\frac{13}{5}\normalsize ,4[/latex]

ⓐ [latex]4[/latex]
ⓑ [latex]-5,-\sqrt{4},4[/latex]
ⓒ [latex]-5,-2\Large\frac{1}{4}\normalsize ,-\sqrt{4},0.\stackrel{\text{-}}{25},\Large\frac{13}{5}\normalsize ,4[/latex]
ⓓ none
ⓔ [latex]-5,-2\Large\frac{1}{4}\normalsize ,-\sqrt{4},0.\stackrel{\text{-}}{25},\Large\frac{13}{5}\normalsize ,4[/latex]

Commutative and Associative Properties

In the following exercises, use the commutative property to rewrite the given expression.

[latex]\text{6+4=____}[/latex]

[latex]\text{-14}\cdot \text{5=____}[/latex]

−14·5 = 5(−14)

[latex]\text{3n=____}[/latex]

[latex]\text{a+8=____}[/latex]

a + 8 = 8 + a

In the following exercises, use the associative property to rewrite the given expression.

[latex]\left(\text{13}\cdot \text{5}\right)\cdot \text{2=_____}[/latex]

[latex]\left(\text{22+7}\right)+\text{3=_____}[/latex]

(22 + 7) + 3 = 22 + (7 + 3)

[latex]\left(\text{4+9x}\right)\text{+x=_____}[/latex]

[latex]\Large\frac{1}{2}\normalsize\left(\text{22y}\right)\text{=_____}[/latex]

[latex]\Large\frac{1}{2}\normalsize\left(22y\right)=\left(\Large\frac{1}{2}\normalsize\cdot 22\right)y[/latex]

In the following exercises, evaluate each expression for the given value.

If [latex]y=\Large\frac{11}{12}[/latex], evaluate:

ⓐ [latex]y+0.7+\left(-y\right)[/latex]

ⓑ [latex]y+\left(-y\right)+0.7[/latex]

If [latex]z=-\Large\frac{5}{3}[/latex], evaluate:

ⓐ [latex]z+5.39+\left(-z\right)[/latex]

ⓑ [latex]z+\left(-z\right)+5.39[/latex]

ⓐ 5.39
ⓑ 5.39

If [latex]k=65[/latex], evaluate:

ⓐ [latex]\Large\frac{4}{9}\normalsize\left(\Large\frac{9}{4}\normalsize k\right)[/latex]

ⓑ [latex]\left(\Large\frac{4}{9}\normalsize\cdot\Large\frac{9}{4}\normalsize\right)k[/latex]

If [latex]m=-13[/latex], evaluate:

ⓐ [latex]-\Large\frac{2}{5}\normalsize\left(\Large\frac{5}{2}\normalsize m\right)[/latex]

ⓑ [latex]\left(-\Large\frac{2}{5}\normalsize\cdot\Large\frac{5}{2}\normalsize\right)m[/latex]

ⓐ 13
ⓑ 13

In the following exercises, simplify using the commutative and associative properties.

[latex]6y+37+\left(-6y\right)[/latex]

[latex]\Large\frac{1}{4}\normalsize +\Large\frac{11}{15}\normalsize +\left(-\Large\frac{1}{4}\normalsize\right)[/latex]

[latex]\Large\frac{11}{15}[/latex]

[latex]\Large\frac{14}{11}\normalsize\cdot\Large\frac{35}{9}\normalsize\cdot\Large\frac{14}{11}[/latex]

[latex]-18\cdot 15\cdot\Large\frac{2}{9}[/latex]

−60

[latex]\left(\Large\frac{7}{12}\normalsize +\Large\frac{4}{5}\normalsize\right)+\Large\frac{1}{5}[/latex]

[latex]\left(3.98d+0.75d\right)+1.25d[/latex]

5.98 d

[latex]-12\left(4m\right)[/latex]

[latex]30\left(\Large\frac{5}{6}\normalsize q\right)[/latex]

25 q

[latex]11x+8y+16x+15y[/latex]

[latex]52m+\left(-20n\right)+\left(-18m\right)+\left(-5n\right)[/latex]

34 m + (−25 n)

Distributive Property

In the following exercises, simplify using the distributive property.

[latex]7\left(x+9\right)[/latex]

[latex]9\left(u - 4\right)[/latex]

9y − 36

[latex]-3\left(6m - 1\right)[/latex]

[latex]-8\left(-7a - 12\right)[/latex]

56a + 96

[latex]\Large\frac{1}{3}\normalsize\left(15n - 6\right)[/latex]

[latex]\left(y+10\right)\cdot p[/latex]

yp + 10p

[latex]\left(a - 4\right)-\left(6a+9\right)[/latex]

[latex]4\left(x+3\right)-8\left(x - 7\right)[/latex]

−4x + 68

In the following exercises, evaluate using the distributive property.

If [latex]u=2[/latex], evaluate

ⓐ [latex]3\left(8u+9\right)\text{and}[/latex]

ⓑ [latex]3\cdot 8u+3\cdot 9[/latex] to show that [latex]3\left(8u+9\right)=3\cdot 8u+3\cdot 9[/latex]

If [latex]n=\Large\frac{7}{8}[/latex], evaluate

ⓐ [latex]8\left(n+\Large\frac{1}{4}\normalsize\right)[/latex] and

ⓑ [latex]8\cdot n+8\cdot\Large\frac{1}{4}[/latex] to show that [latex]8\left(n+\Large\frac{1}{4}\normalsize\right)=8\cdot n+8\cdot\Large\frac{1}{4}[/latex]

ⓐ 9
ⓑ 9

If [latex]d=14[/latex], evaluate

ⓐ [latex]-100\left(0.1d+0.35\right)[/latex] and

ⓑ [latex]-100\cdot \left(0.1d\right)+\left(-100\right)\left(0.35\right)[/latex] to show that [latex]-100\left(0.1d+0.35\right)=-100\cdot \left(0.1d\right)+\left(-100\right)\left(0.35\right)[/latex]

If [latex]y=-18[/latex], evaluate

ⓐ [latex]-\left(y - 18\right)[/latex] and

ⓑ [latex]-y+18[/latex] to show that [latex]-\left(y - 18\right)=-y+18[/latex]

ⓐ 36
ⓑ 36

Properties of Identities, Inverses, and Zero

In the following exercises, identify whether each example is using the identity property of addition or multiplication.

[latex]-35\left(1\right)=-35[/latex]

[latex]29+0=29[/latex]

identity property of addition

[latex]\left(6x+0\right)+4x=6x+4x[/latex]

[latex]9\cdot 1+\left(-3\right)=9+\left(-3\right)[/latex]

identity property of multiplication

In the following exercises, find the additive inverse.

[latex]-32[/latex]

[latex]19.4[/latex]

−19.4

[latex]\Large\frac{3}{5}[/latex]

[latex]-\Large\frac{7}{15}[/latex]

[latex]\Large\frac{7}{15}[/latex]

In the following exercises, find the multiplicative inverse.

[latex]\Large\frac{9}{2}[/latex]

[latex]-5[/latex]

[latex]-\Large\frac{1}{5}[/latex]

[latex]\Large\frac{1}{10}[/latex]

[latex]-\Large\frac{4}{9}[/latex]

[latex]-\Large\frac{9}{4}[/latex]

In the following exercises, simplify.

[latex]83\cdot 0[/latex]

[latex]\Large\frac{0}{9}[/latex]

0

[latex]\Large\frac{5}{0}[/latex]

[latex]0\div\Large\frac{2}{3}[/latex]

0

[latex]43+39+\left(-43\right)[/latex]

[latex]\left(n+6.75\right)+0.25[/latex]

n + 7

[latex]\Large\frac{5}{13}\normalsize\cdot 57\cdot\Large\frac{13}{5}[/latex]

[latex]\Large\frac{1}{6}\normalsize\cdot 17\cdot 12[/latex]

34

[latex]\Large\frac{2}{3}\normalsize\cdot 28\cdot\Large\frac{3}{7}[/latex]

[latex]9\left(6x - 11\right)+15[/latex]

54x − 84

Systems of Measurement

In the following exercises, convert between U.S. units. Round to the nearest tenth.

A floral arbor is [latex]7[/latex] feet tall. Convert the height to inches.

A picture frame is [latex]42[/latex] inches wide. Convert the width to feet.

3.5 feet

Kelly is [latex]5[/latex] feet [latex]4[/latex] inches tall. Convert her height to inches.

A playground is [latex]45[/latex] feet wide. Convert the width to yards.

15 yards

The height of Mount Shasta is [latex]14,179[/latex] feet. Convert the height to miles.

Shamu weighs [latex]4.5[/latex] tons. Convert the weight to pounds.

9000 pounds

The play lasted [latex]1\Large\frac{3}{4}[/latex] hours. Convert the time to minutes.

How many tablespoons are in a quart?

64 tablespoons

Naomi’s baby weighed [latex]5[/latex] pounds [latex]14[/latex] ounces at birth. Convert the weight to ounces.

Trinh needs [latex]30[/latex] cups of paint for her class art project. Convert the volume to gallons.

1.9 gallons

In the following exercises, solve, and state your answer in mixed units.

John caught [latex]4[/latex] lobsters. The weights of the lobsters were [latex]1[/latex] pound [latex]9[/latex] ounces, [latex]1[/latex] pound [latex]12[/latex] ounces, [latex]4[/latex] pounds [latex]2[/latex] ounces, and [latex]2[/latex] pounds [latex]15[/latex] ounces. What was the total weight of the lobsters?

Every day last week, Pedro recorded the amount of time he spent reading. He read for [latex]50,25,83,45,32,60,\text{and}135[/latex] minutes. How much time, in hours and minutes, did Pedro spend reading?

7 hours 10 minutes

Fouad is [latex]6[/latex] feet [latex]2[/latex] inches tall. If he stands on a rung of a ladder [latex]8[/latex] feet [latex]10[/latex] inches high, how high off the ground is the top of Fouad’s head?

Dalila wants to make pillow covers. Each cover takes [latex]30[/latex] inches of fabric. How many yards and inches of fabric does she need for [latex]4[/latex] pillow covers?

3 yards, 12 inches

In the following exercises, convert between metric units.

Donna is [latex]1.7[/latex] meters tall. Convert her height to centimeters.

Mount Everest is [latex]8,850[/latex] meters tall. Convert the height to kilometers.

8.85 kilometers

One cup of yogurt contains [latex]488[/latex] milligrams of calcium. Convert this to grams.

One cup of yogurt contains [latex]13[/latex] grams of protein. Convert this to milligrams.

13,000 milligrams

Sergio weighed [latex]2.9[/latex] kilograms at birth. Convert this to grams.

A bottle of water contained [latex]650[/latex] milliliters. Convert this to liters.

0.65 liters

In the following exercises, solve.

Minh is [latex]2[/latex] meters tall. His daughter is [latex]88[/latex] centimeters tall. How much taller, in meters, is Minh than his daughter?

Selma had a [latex]\text{1-liter}[/latex] bottle of water. If she drank [latex]145[/latex] milliliters, how much water, in milliliters, was left in the bottle?

855 milliliters

One serving of cranberry juice contains [latex]30[/latex] grams of sugar. How many kilograms of sugar are in [latex]30[/latex] servings of cranberry juice?

One ounce of tofu provides [latex]2[/latex] grams of protein. How many milligrams of protein are provided by [latex]5[/latex] ounces of tofu?

10,000 milligrams

In the following exercises, convert between U.S. and metric units. Round to the nearest tenth.

Majid is [latex]69[/latex] inches tall. Convert his height to centimeters.

A college basketball court is [latex]84[/latex] feet long. Convert this length to meters.

25.6 meters

Caroline walked [latex]2.5[/latex] kilometers. Convert this length to miles.

Lucas weighs [latex]78[/latex] kilograms. Convert his weight to pounds.

171.6 pounds

Steve’s car holds [latex]55[/latex] liters of gas. Convert this to gallons.

A box of books weighs [latex]25[/latex] pounds. Convert this weight to kilograms.

11.4 kilograms

In the following exercises, convert the Fahrenheit temperatures to degrees Celsius. Round to the nearest tenth.

[latex]95{^\circ F}[/latex]

[latex]23{^\circ F}[/latex]

−5°C

[latex]20{^\circ F}[/latex]

[latex]64{^\circ F}[/latex]

17.8°C

In the following exercises, convert the Celsius temperatures to degrees Fahrenheit. Round to the nearest tenth.

[latex]30{^\circ C}[/latex]

[latex]-5{^\circ C}[/latex]

23°F

[latex]-12{^\circ C}[/latex]

[latex]24{^\circ C}[/latex]

75.2°F

Chapter Practice Test

For the numbers [latex]\text{0.18349\ldots },0.\stackrel{\text{-}}{\text{2}},1.67[/latex], list the ⓐ rational numbers and ⓑ irrational numbers.

Is [latex]\sqrt{144}[/latex] rational or irrational?

[latex]\sqrt{144}=12\text{therefore rational.}[/latex]

From the numbers [latex]-4,-1\Large\frac{1}{2}\normalsize ,0,\Large\frac{5}{8}\normalsize ,\sqrt{2},7[/latex], which are ⓐ integers ⓑ rational ⓒ irrational ⓓ real numbers?

Rewrite using the commutative property: [latex]x\cdot \text{14=_________}[/latex]

x·14 = 14·x

Rewrite the expression using the associative property: [latex]\left(y+6\right)\text{+3=_______________}[/latex]

Rewrite the expression using the associative property: [latex]\left(8\cdot 2\right)\cdot \text{5=___________}[/latex]

(8·2)·3 = 8·(2·3)

Evaluate [latex]\Large\frac{3}{16}\normalsize\left(\Large\frac{16}{3}\normalsize n\right)[/latex] when [latex]n=42[/latex].

For the number [latex]\Large\frac{2}{5}[/latex] find the ⓐ additive inverse ⓑ multiplicative inverse.

ⓐ [latex]-\Large\frac{2}{5}[/latex]
ⓑ [latex]\Large\frac{5}{2}[/latex]

In the following exercises, simplify the given expression.

[latex]\Large\frac{3}{4}\normalsize\left(-29\right)\left(\Large\frac{4}{3}\normalsize\right)[/latex]

[latex]-3+15y+3[/latex]

15y

[latex]\left(1.27q+0.25q\right)+0.75q[/latex]

[latex]\left(\Large\frac{8}{15}\normalsize +\Large\frac{2}{9}\normalsize\right)+\Large\frac{7}{9}[/latex]

[latex]\Large\frac{23}{15}[/latex]

[latex]-18\left(\Large\frac{3}{2}\normalsize n\right)[/latex]

[latex]14y+\left(-6z\right)+16y+2z[/latex]

30y − 4z

[latex]9\left(q+9\right)[/latex]

[latex]6\left(5x - 4\right)[/latex]

30x − 24

[latex]-10\left(0.4n+0.7\right)[/latex]

[latex]\Large\frac{1}{4}\normalsize\left(8a+12\right)[/latex]

2a + 3

[latex]m\left(n+2\right)[/latex]

[latex]8\left(6p - 1\right)+2\left(9p+3\right)[/latex]

66p − 2

[latex]\left(12a+4\right)-\left(9a+6\right)[/latex]

[latex]\Large\frac{0}{8}[/latex]

0

[latex]\Large\frac{4.5}{0}[/latex]

[latex]0\div \left(\Large\frac{2}{3}\normalsize\right)[/latex]

0

In the following exercises, solve using the appropriate unit conversions.

Azize walked [latex]4\Large\frac{1}{2}[/latex] miles. Convert this distance to feet. [latex]\text{(1 mile}=\text{5,280 feet).}[/latex]

One cup of milk contains [latex]276[/latex] milligrams of calcium. Convert this to grams. [latex]\text{(1 milligram}=\text{0.001 gram)}[/latex]

.276 grams

Larry had [latex]5[/latex] phone customer phone calls yesterday. The calls lasted [latex]28,44,9,75,\text{and}55[/latex] minutes. How much time, in hours and minutes, did Larry spend on the phone? [latex]\text{(1 hour}=\text{60 minutes)}[/latex]

Janice ran [latex]15[/latex] kilometers. Convert this distance to miles. Round to the nearest hundredth of a mile. [latex]\text{(1 mile}=\text{1.61 kilometers)}[/latex]

9.317 miles

Yolie is [latex]63[/latex] inches tall. Convert her height to centimeters. Round to the nearest centimeter. [latex]\text{(1 inch}=\text{2.54 centimeters)}[/latex]

Use the formula [latex]F=\Large\frac{9}{5}\normalsize C+32[/latex] to convert [latex]35{^\circ C}[/latex] to degrees [latex]\text{F}[/latex]

95°F