Simplifying Real Numbers With Exponents

Learning Outcomes

Simplify expressions with exponents and integer bases
Simplify expressions with exponents and rational bases

Remember that an exponent indicates repeated multiplication of the same quantity. For example, ${2}^{4}$ means to multiply four factors of $2$ , so ${2}^{4}$ means $2\cdot 2\cdot 2\cdot 2$ . This format is known as exponential notation.

Exponential Notation

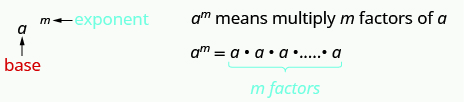
On the left side, a raised to the m is shown. The m is labeled in blue as an exponent. The a is labeled in red as the base. On the right, it says a to the m means multiply m factors of a. Below this, it says a to the m equals a times a times a times a, with m factors written below in blue.
This is read $a$ to the ${m}^{\mathrm{th}}$ power.

In the expression ${a}^{m}$ , the exponent tells us how many times we use the base $a$ as a factor.

On the left side, 7 to the 3rd power is shown. Below is 7 times 7 times 7, with 3 factors written below. On the right side, parentheses negative 8 to the 5th power is shown. Below is negative 8 times negative 8 times negative 8 times negative 8 times negative 8, with 5 factors written below.
Before we begin working with variable expressions containing exponents, let’s simplify a few expressions involving only numbers.

example

Simplify:

1. ${5}^{3}$
2. ${9}^{1}$

Solution

1.
	${5}^{3}$
Multiply $3$ factors of $5$ .	$5\cdot 5\cdot 5$
Simplify.	$125$

2.
	${9}^{1}$
Multiply $1$ factor of $9$ .	$9$

try it

example

Simplify:

1. ${\left({\Large\frac{7}{8}}\right)}^{2}$
2. ${\left(0.74\right)}^{2}$

Show Solution

Solution

1.
	${\left({\Large\frac{7}{8}}\right)}^{2}$
Multiply two factors.	$\left({\Large\frac{7}{8}}\right)\left({\Large\frac{7}{8}}\right)$
Simplify.	${\Large\frac{49}{64}}$

2.
	${\left(0.74\right)}^{2}$
Multiply two factors.	$\left(0.74\right)\left(0.74\right)$
Simplify.	$0.5476$

try it

example

Simplify:

1. ${\left(-3\right)}^{4}$
2. ${-3}^{4}$

Show Solution

Solution

1.
	${\left(-3\right)}^{4}$
Multiply four factors of $−3$ .	$\left(-3\right)\left(-3\right)\left(-3\right)\left(-3\right)$
Simplify.	$81$

2.
	${-3}^{4}$
Multiply two factors.	$-\left(3\cdot 3\cdot 3\cdot 3\right)$
Simplify.	$-81$

Notice the similarities and differences in parts 1 and 2. Why are the answers different? In part 1 the parentheses tell us to raise the $(−3)$ to the $4$ ^th power. In part 2 we raise only the $3$ to the $4$ ^th power and then find the opposite.

Module 10: Polynomials