Solutions to Differential Equations

Learning Outcomes

  • Identify the order of a differential equation
  • Explain what is meant by a solution to a differential equation
  • Distinguish between the general solution and a particular solution of a differential equation

General Differential Equations

Consider the equation [latex]{y}^{\prime }=3{x}^{2}[/latex], which is an example of a differential equation because it includes a derivative. There is a relationship between the variables [latex]x[/latex] and [latex]y\text{:}y[/latex] is an unknown function of [latex]x[/latex]. Furthermore, the left-hand side of the equation is the derivative of [latex]y[/latex]. Therefore we can interpret this equation as follows: Start with some function [latex]y=f\left(x\right)[/latex] and take its derivative. The answer must be equal to [latex]3{x}^{2}[/latex]. What function has a derivative that is equal to [latex]3{x}^{2}?[/latex] One such function is [latex]y={x}^{3}[/latex], so this function is considered a solution to a differential equation.

Definition

A differential equation is an equation involving an unknown function [latex]y=f\left(x\right)[/latex] and one or more of its derivatives. A solution to a differential equation is a function [latex]y=f\left(x\right)[/latex] that satisfies the differential equation when [latex]f[/latex] and its derivatives are substituted into the equation.

Some examples of differential equations and their solutions appear in the following table.

 
Equation Solution
[latex]y^{\prime} =2x[/latex] [latex]y={x}^{2}[/latex]
[latex]y^{\prime} +3y=6x+11[/latex] [latex]y={e}^{-3x}+2x+3[/latex]
[latex]y^{\prime} \prime -3y^{\prime} +2y=24{e}^{-2x}[/latex] [latex]y=3{e}^{x}-4{e}^{2x}+2{e}^{-2x}[/latex]

Note that a solution to a differential equation is not necessarily unique, primarily because the derivative of a constant is zero. For example, [latex]y={x}^{2}+4[/latex] is also a solution to the first differential equation in the table. We will return to this idea a little bit later in this section. First, we briefly review the rules for derivatives of exponential functions, and then explore what it means for a function to be a solution to a differential equation.

Recall: Derivatives of Exponential Functions

  1. [latex]\frac{d}{dx} \left( e^x \right) = e^x[/latex]
  2. [latex]\frac{d}{dx} \left( e^{g(x)} \right) = e^{g(x)}g'(x)[/latex]    (this is the chain rule applied to the derivative of an exponential function)

Example: Verifying Solutions of Differential Equations

Verify that the function [latex]y={e}^{-3x}+2x+3[/latex] is a solution to the differential equation [latex]{y}^{\prime }+3y=6x+11[/latex].

Watch the following video to see the worked solution to Example: Verifying Solutions of Differential Equations

You can view the transcript for “4.1.2” here (opens in new window).

try it

Verify that [latex]y=2{e}^{3x}-2x - 2[/latex] is a solution to the differential equation [latex]{y}^{\prime }-3y=6x+4[/latex].

It is convenient to define characteristics of differential equations that make it easier to talk about them and categorize them. The most basic characteristic of a differential equation is its order.

Definition

The order of a differential equation is the highest order of any derivative of the unknown function that appears in the equation.

Example: Identifying the Order of a Differential Equation

What is the order of each of the following differential equations?

  1. [latex]{y}^{\prime }-4y={x}^{2}-3x+4[/latex]
  2. [latex]{x}^{2}y\text{'''}-3xy\text{''}+x{y}^{\prime }-3y=\sin{x}[/latex]
  3. [latex]\frac{4}{x}{y}^{\left(4\right)}-\frac{6}{{x}^{2}}y\text{''}+\frac{12}{{x}^{4}}y={x}^{3}-3{x}^{2}+4x - 12[/latex]

Watch the following video to see the worked solution to Example: Identifying the Order of a Differential Equation

You can view the transcript for “4.1.1” here (opens in new window).

try it

What is the order of the following differential equation?

[latex]\left({x}^{4}-3x\right){y}^{\left(5\right)}-\left(3{x}^{2}+1\right){y}^{\prime }+3y=\sin{x}\cos{x}[/latex]

General and Particular Solutions

We already noted that the differential equation [latex]{y}^{\prime }=2x[/latex] has at least two solutions: [latex]y={x}^{2}[/latex] and [latex]y={x}^{2}+4[/latex]. The only difference between these two solutions is the last term, which is a constant. What if the last term is a different constant? Will this expression still be a solution to the differential equation? In fact, any function of the form [latex]y={x}^{2}+C[/latex], where [latex]C[/latex] represents any constant, is a solution as well. The reason is that the derivative of [latex]{x}^{2}+C[/latex] is [latex]2x[/latex], regardless of the value of [latex]C[/latex]. It can be shown that any solution of this differential equation must be of the form [latex]y={x}^{2}+C[/latex]. This is an example of a general solution to a differential equation. A graph of some of these solutions is given in Figure 1. (Note: in this graph we used even integer values for [latex]C[/latex] ranging between [latex]-4[/latex] and [latex]4[/latex]. In fact, there is no restriction on the value of [latex]C[/latex]; it can be an integer or not.)

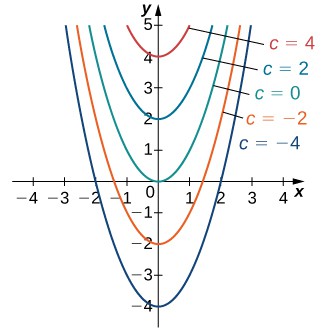
A graph of a family of solutions to the differential equation y’ = 2 x, which are of the form y = x ^ 2 + C. Parabolas are drawn for values of C: -4, -2, 0, 2, and 4.

Figure 1. Family of solutions to the differential equation [latex]{y}^{\prime }=2x[/latex].

In this example, we are free to choose any solution we wish; for example, [latex]y={x}^{2}-3[/latex] is a member of the family of solutions to this differential equation. This is called a particular solution to the differential equation. A particular solution can often be uniquely identified if we are given additional information about the problem.

Example: Finding a Particular Solution

Find the particular solution to the differential equation [latex]{y}^{\prime }=2x[/latex] passing through the point [latex]\left(2,7\right)[/latex].

Watch the following video to see the worked solution to Example: Finding a Particular Solution

You can view the transcript for “4.1.3” here (opens in new window).

try it

Find the particular solution to the differential equation

[latex]{y}^{\prime }=4x+3[/latex]

 

passing through the point [latex]\left(1,7\right)[/latex], given that [latex]y=2{x}^{2}+3x+C[/latex] is a general solution to the differential equation.

Try It